Les verres de lunettes livrés aux opticiens par les fabricants se présentent sous la forme de palets circulaires de diamètres variant entre 50 et 85 mm. En fonction de la forme de la monture, de la morphologie du porteur et de la compensation prescrite, ces palets sont meulés (on parle alors de verres taillés).
Les formes des verres sont extrêmement variées. Au tout début de la lunetterie elles étaient circulaires ou elliptiques et puis, la mode aidant, elles ont subi toutes sortes de variations.
Aujourd'hui les stylistes dessinent les formes et les infographistes les mettent en équation à l'écran avec les outils modernes de la C.A.O. Le dessin vectoriel et sa cohorte de splines est un outil parmi d'autres.
Un modèle simple de calibre est constitué par un ensemble de quatre arcs de cercle raccordés tangentiellement. C'est celui qui va être développé ci-après.
A. Macros préalables
1. Cercle tangent à deux cercles donnés et passant par un point de l'un d'eux.
La construction est précisée sur le schéma ci-dessous.
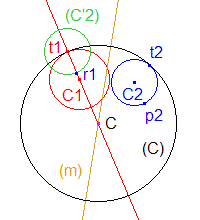 |
Soit les cercles (C1) et (C2) et le point t1 sur (C1).
a. On trace la droite t1C1, ainsi que la demi-droite t1C1.
b. L'outil compas permet ensuite de reporter le rayon de C2p2 du cercle (C2) en t1.
c. L'intersection de ce cercle avec la demi-droite t1C1 est appelée r1.
d. La médiatrice (m) de r1C2 coupe la droite t1C1 en C, centre du cercle recherché.
e. Ce cercle (C) est tracé et son intersection (double) avec (C2) est appelée t2. |
2. Arc de cercle définissant un segment de cercle ne contenant pas un point intérieur au cercle.
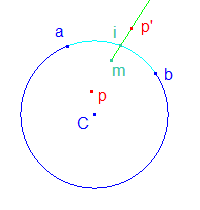 |
Deux points a et b définissent un arc du cercle C. Le point p est à l'intérieur du cercle. On souhaite tracer l'arc associé au segment de cercle (ab) ne contenant pas p.
a. L'outil milieu donne le milieu m de ab.
b. La symétrie centrale de centre m, transforme p en p'.
c. La demi-droite mp' coupe le cercle (C) en i.
d. L'arc recherché est aib.
|
3. Tangente(s) à un arc de cercle, parallèle(s) à une direction donnée.
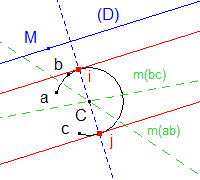 |
On se donne un arc de cercle (abc) et une droite (D).
(abc) est un grand arc, afin de prévoir le cas de figure où le problème admet deux solutions.
a. Les médiatrices de ab et bc, m(ab) et m(bc) se coupent en C, centre de courbure de l'arc.
b. La perpendiculaire menée de C à la droite (D) coupe l'arc suivant i et j.
c. Les parallèles en ces points à (D) donnent les tangentes recherchées.
|
B. La figure CalibreVerreLunettes
Les deux cercles de base sont (C1) et (C3) dont les centres sont placés sur la droite (D).
(D) peut tourner autour de M.
Les quatre points de raccordement sont T1, T2, T3 et T4.
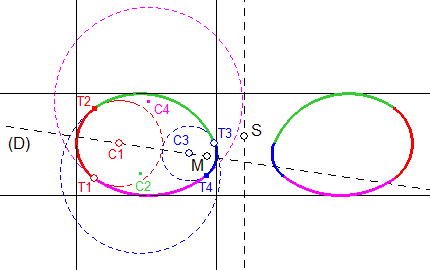
La figure a été fabriquée de la sorte :
- On commence par tracer la droite (D) qui peut tourner autour du point M.
- Les deux cercles de base (C1) et (C3) ont leurs centres sur (D), de part et d'autre de M.
- Les points de raccordement des deux cercles par des segments de droite sont ensuite construits :
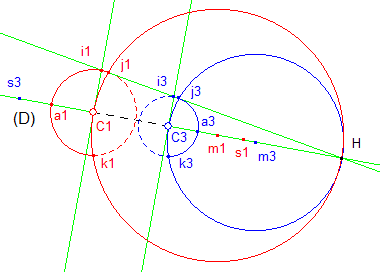
- Perpendiculaires à (D) en C1 et C3
- Intersection supérieure avec chacun des cercles (i1 et i3)
- Intersection H de i1i3 avec (D)
- Milieux m1 et m3 de C1H et C3H
- Cercles de rayons C1m1 et C3m3
- Intersections respectives de ces cercles avec les cercles (C1) et (C3) : j1, k1 et j3, k3.
- Les symétriques de C1 et C3 par rapport à C3 et C1 sont s1 et s3.
- Les demi-droites C1s3 et C3s1 coupent les cercles (C1) et (C3) respectivement en a1 et a3
- Cela permet de tracer les arcs de cercle (j1a1k1) et (j3a3k3) sur lesquels vont se déplacer les points courants T1 et T3, MAIS...
Pour éviter une anomalie de tracé quand le rayon des cercles de raccordement devient infini, les arcs (j1a1k1) et (j3a3k3) sont réduits artificiellement de la manière suivante :
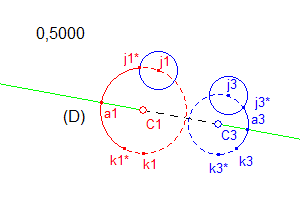 |
- Un nombre, par exemple 0,5 est reporté par l'outil compas en j1 et j3.
- Les cercles correspondants coupent les arcs (j1a1k1) et (j3a3k3) en j1* et j3*.
- Les symétriques de j1* et j3* par rapport à (D) sont k1* et k3*.
- De nouveaux arcs (j1*a1k1*) et (j3*a3k3*) sont alors créés sur lesquels vont être placés les points courants T1 et T3.
- Le nombre est minimisé (0,0001, par exemple).
|
 |
- On applique la macro définie en A)1) : cercle_tangent_a_deux_cercles.mac à (C1), T1, (C3), et à (C3), T3, (C1) ; on obtient ainsi les cercles (C2) et (C4), ainsi que les points T2 et T4.
- L'intersection des diagonales T1T3 et T2T4 est appelée i.
- La macro définie en A)2) : ArcExterieur.mac appliquée à (C2), T2, T3, i et à (C4), T3, T4, i nous donne les deux arcs raccordant les cercles (C1) et (C3).
On vérifie le raccordement rectiligne sur l'exemple ci-dessous où T3 est en butée en j3* (T2 coïncide alors avec j1*).
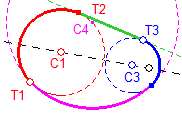
|
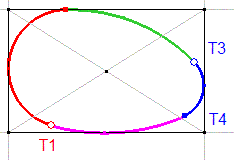 |
- La macro Tangente_s_Arc.mac (cf.(A)3)) est appliquée aux arcs (T2T3) et (T4T1) par rapport à une droite parallèle à l'axe des x, aux arcs (T1T2) et (T3T4), par rapport à une droite parallèle à l'axe des y.
- Les intersections de ces droites déinissent la mise en boîte du calibre (on parle de système boxing) qui permet de lui associer une largeur, une hauteur, un centre.
- Le centre est obtenu en recherchant l'intersection des deux diagonales du rectangle.
Tous les cas de figure doivent être envisagés.
|
|