Les copies et reproductions de ce document, destinées à une utilisation collective, ne sont pas autorisées.

10. Viseur à mise au point interne (Contrôle d'Optique du 2 février 2001) Un viseur à mise au point interne comprend trois lentilles minces : - l'objectif L1, de focale f '1 = + 100 mm, ouvert à f / 8 ; - le véhicule L2, de focale f '2 = - 200 mm ; - l'oculaire L3, convergent et de grossissement commercial 12,5. Un réticule fixe Ré est placé à 200 mm de L1. Le diaphragme d'ouverture DO est constitué par L1. Le diaphragme de champ DC, de diamètre 12 mm, est placé dans le plan du réticule. On suppose que l'observateur emmétrope n'accommode pas. La mise au point sur un plan objet [A] est effectuée en déplaçant le véhicule L2 entre L1 et le réticule. La distance séparant L1 de L2 est notée x. L1 et L2 donnent de A une image A2 qui se forme dans le plan du réticule. 1) x = 0 mm 1.1 Calculer la position AL1 du plan objet. Que constate-t-on ? Aurait-on pu prévoir ce résultat ? 1.2 Quel est alors le grossissement du viseur ? 2) x = 200 mm 2.1 Calculer la position du plan objet. 2.2 Quelle est la puissance du viseur ? 2.3 Que se passerait-il si la lentille L2 était ôtée du viseur ? Justifier la réponse. 3) x variable 3.1 La proximité du plan visé en fonction de la distance L1L2 est donnée en annexe par la courbe A = f(x), avec A = 1/AL1 (Figure 1) La position de L2 est repérée par rapport à une règle graduée en dioptrie. Les graduations sont-elles plus resserrées pour x = 0, x = 100 ou x = 200 ? Justifier la réponse. 3.2 Quel diamètre faudrait-il donner à L2 pour que le champ du viseur dans le plan du réticule soit indépendant de x ? On pourra raisonner à partir de la Figure 2 donnée en annexe, où la courbe (C) représente la variation du diamètre de la pupille en fonction de sa position. 3.3 Quand il y a un défaut de mise au point, l'image d'un point objet dans le plan du réticule est une tache de diffusion de diamètre ε'. L'observateur voit l'image nette si l'image de ε' à travers l'oculaire ne dépasse pas un angle de 4.10-4 radian. En déduire la profondeur de champ pour les cas x = 100 mm et x = 200 mm.

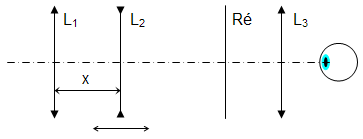
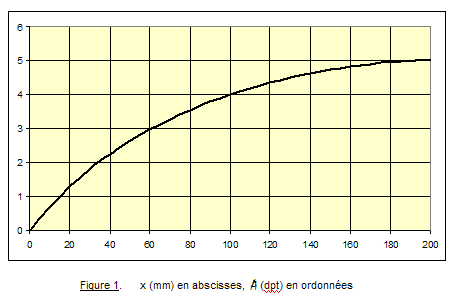
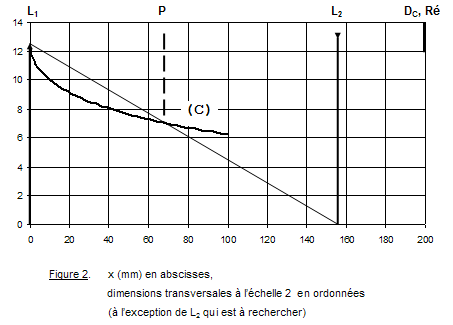
1) 1.1 Les conjugaisons à travers les deux lentilles L1 et L2 sont : 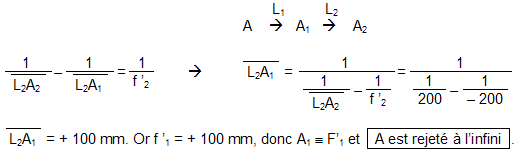On aurait pu remarquer que, comme les lentilles L1 et L2 sont accolées et ont pour vergences respectives + 10 et - 5 , le doublet (L1, L2) est assimilable à une lentille mince L12 de vergence : D12 = D1 + D2 = 10 - 5 = + 5 δ. Sa focale est f '12 = 1 / D12 = 1 / 5 m soit + 200 mm. A2 est confondu avec le foyer principal image du doublet, A2 ≡ F'12. A est à l'infini. 1.2 Comme l'observateur emmétrope n'accommode pas, l'image instrumentale A' est rejetée à l'infini et le viseur est un système afocal. Le grossissement est le rapport, en valeur absolue, du diamètre apparent de l'image observée à travers le viseur θ' au diamètre apparent de l'objet observé à l'œil nu θ : G = |θ' / θ| . Il est égal au rapport de la focale de l'objectif à la focale de l'oculaire : G = f 'ob / f 'oc Dans cette formule, l'objectif est représenté par le doublet (L1, L2) et l'oculaire par L3. Le grossissement commercial de l'oculaire est égal à sa puissance intrinsèque divisée par quatre dioptries. Comme l'oculaire est convergent, sa puissance intrinsèque est égale à sa vergence. 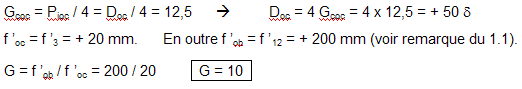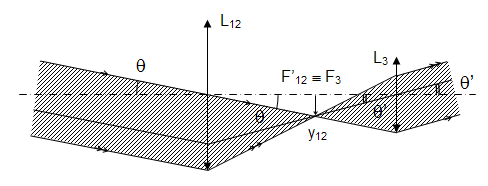2) 2.1 La lentille L2 est appliquée contre le réticule. A1 et A2 sont confondus (les plans principaux d'une lentille mince sont confondus avec le plan de la lentille). A1 et X'1 (point antiprincipal* image de L1) sont également confondus. A est confondu avec le point antiprincipal objet de L1 : A ≡ X1. * Les points antiprincipaux d'un système optique sont deux points conjugués X et X', tels que : gy (X, X') = - 1. Les relations de grandissement de Newton permettent de montrer que ces points sont symétriques des points principaux par rapport aux foyers. Dans le cas d'une lentille mince, ils sont situés à une distance 2 f ' de part et d'autre de la lentille. 2.2 La puissance du viseur est le rapport, en valeur absolue, du diamètre apparent θ' de l'image à la taille y de l'objet : P = |θ' / y|. 2.3 Si la lentille L2 est ôtée du viseur Voir justification sur le schéma ci-après. 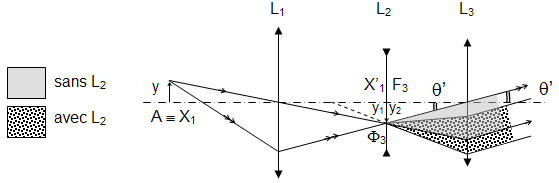Le bord de l'image objective y1 appartient au plan focal objet de l'oculaire qu'il y ait ou non la lentille L2. Son image à travers L3 est dans le direction θ' indépendamment de la présence de L2. L2 fait tourner le faisceau conique (grisé sur le schéma ci-dessus), le sommet de ce faisceau restant fixe et confondu avec un foyer secondaire objet de L3, Φ3. 3) 3.1 La construction des graduations dioptriques montre que 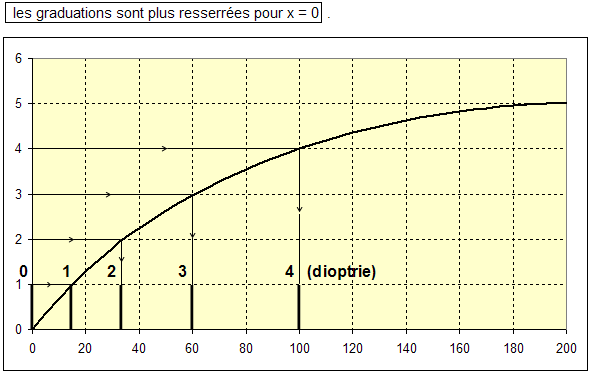On l'obtient par double conjugaison de A2 dans l'espace objet du viseur. 3.2 P est le conjugué de L1 à travers L2. Comme la lentille L2 est divergente et L1 réel, P est une image virtuelle droite plus petite que L1. Quand L2 se déplace entre L1 et le réticule Ré, P se déplace entre L1 et le milieu de L1Ré. La courbe de la figure 2 représente la variation de rayon d'ouverture de P : pour une position quelconque de L2 l'intersection de la droite joignant le bord supérieur de L1 et le centre optique de L2 avec la courbe donne à la fois le rayon d'ouverture de P et la position de P. Dans l'espace image de L2 le faisceau utile à la limite du champ (bord de DC) est un faisceau conique de sommet confondu avec le bord de DC et qui s'appuie sur la pupille intermédiaire P. Représentons sur la figure 2 le demi-faisceau utile pour les trois positions : 1. x = 0 mm ; 2. x quelconque ; 3. x = 200 mm. Il apparaît que le rayon supérieur de ce demi-faisceau pivote autour du bord supérieur de DC et que l'intersection de ce rayon avec le plan de L2 décrit une courbe ( Γ ) dont le point le plus éloigné de l'axe optique correspond au bord supérieur de L1. 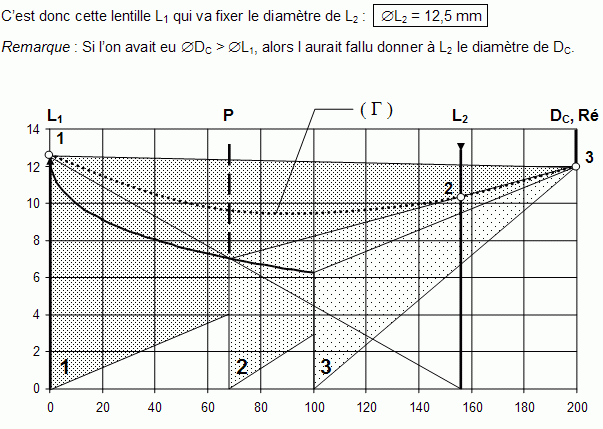3.3 ε' = f '3 . θ' = 20 x 4 x 10- 4 = 80 10- 4 mm, soit 8 μm. Le conjugué objet de ε' est obtenu à partir du grandissement | gy(A, A2)|. Pour x = 100 mm, 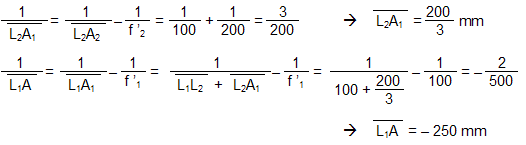On aurait pu lire directement la position de A sur la courbe (4 dioptries de proximité correspondent effectivement à 250 mm). Le grandissement transversal est : 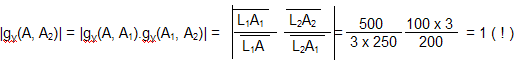Pour x = 200 mm Comme A et A2 sont les points antiprincipaux de L1, on aura de même |gy(A, A2)| = 1 ( ! ! ) Le diamètre de la pupille d'entrée est ØPe = ØL1 / 8 = 100 / 8 = 12, 5 mm. Compte-tenu des grandissements égaux à 1, le conjugué objet du cercle de tolérance a pour diamètre Øε = 8 μm. Comme cette valeur est très petite par rapport à ØPe, la profondeur de champ est approximativement symétrique par rapport au plan objet [A].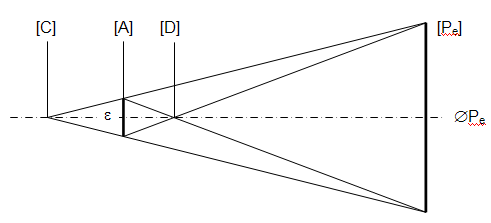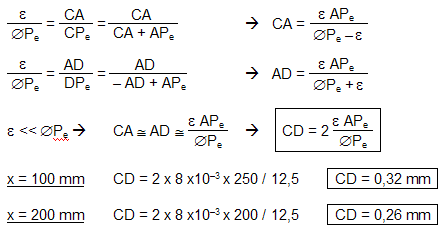

à suivre ...

DinOOptic | Optique géométrique | Début exercice