4. Loupe de Visolett
Une loupe de Visolett est une lentille plan-convexe dont l'épaisseur est égale au quatre tiers du rayon de courbure de la face convexe. Elle est posée, face plane contre l'objet que l'on veut observer (texte, timbre poste, etc.).
Indice du verre : n = 1,5
Rayon de courbure du dioptre convexe : R = 25 mm.
1) Déterminer les points cardinaux de la loupe.
2) Calculer la position de l'image d'un objet placé contre le dioptre plan.
3) Quel est le grandissement transversal de la loupe gy ?
4) Quel est son grossissement commercial Gc ?
5) Etudier la variation du grossissement réel quand l'observateur se place à une distance de l'objet comprise entre 25 cm et 45 cm.
6) Conclure, en comparant G, gy et Gc.
7) De combien faudrait-il éloigner la loupe de l'objet pour que le grandissement devienne égal à 2,5 ?
1) Pour un faisceau objet parallèle à l'axe optique, la lentille plan-convexe se comporte comme un dioptre sphérique. Ses points cardinaux-image sont donc ceux de ce dioptre sphérique. Le point principal image H' est confondu avec le sommet S2 du dioptre, et le foyer principal image F', confondu avec le foyer principal image du dioptre F'2.
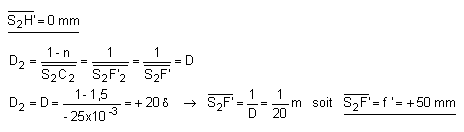
Le point principal objet H de la loupe est le conjugué objet de H' à travers la loupe, mais comme H' est confondu avec S2, H est le conjugué objet de S2 à travers le dioptre plan.
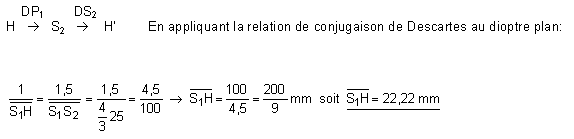
Comme les milieux extrêmes sont identiques, les focales objet et image sont opposées.
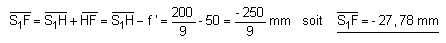
Remarque :
On aurait pu calculer les points cardinaux à partir des formules de Gullstrand :
La première formule donne D = D2 car D1 = 0 ;
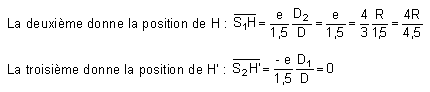
Les positions des foyers s'obtiennent ensuite par décomposition algébrique.
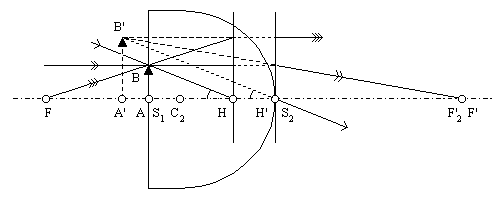
Le schéma ci-dessus précise la construction de l'image d'un objet AB :
Le point B est défini par un rayon parallèle à l'axe optique et un rayon passant par le foyer principal objet F de la loupe.
Les rayons réfractés sont construits par rapport aux plans principaux [H] et [H']. Ils se coupent en B'. Le pied de la perpendiculaire menée de B' à l'axe optique donne A'.
Le rayon incident passant par B et H conserve sa direction après réfraction par la loupe, car les points principaux H et H' sont également points nodaux.
2) La relation de conjugaison de Newton appliquée aux points conjugués A et A' donne :
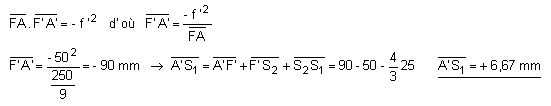
3) La relation de grandissement de Newton appliquée dans l'espace objet de la loupe donne :
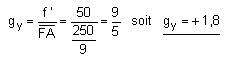
4) Le grossissement commercial de la loupe est défini par le rapport tanq' / tanq25,
où q' représente le diamètre apparent de l'image, et q25 , le diamètre apparent de l'objet s'il était placé à la distance conventionnelle de 25 cm de l'œil.
La loupe est utilisée de façon intrinsèque (objet en [F], ou bien œil de l'observateur en [F']).
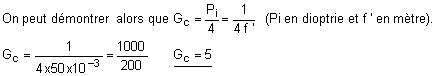
5) Le grossissement réel de la loupe est le rapport tanq' / tanq,
où q et q' sont les diamètres apparents de l'objet et de l'image pour les conditions d'utilisation.
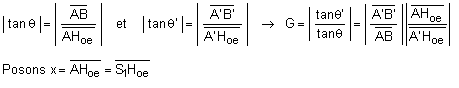
Le premier terme de la décomposition de G correspond au grandissement transversal 1,8.
Comme la position de l'image A' est connue,
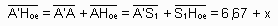
d'où l'on déduit :
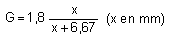
Il s'agit d'une hyperbole équilatère d'asymptotes : x = - 6,67 et G = 1,8
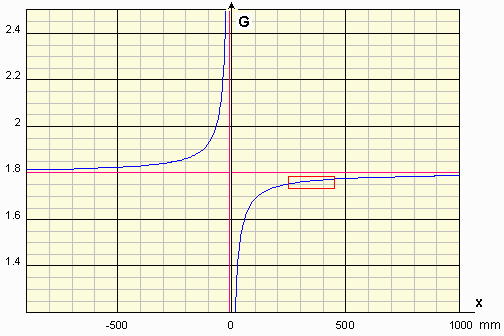
La partie de la courbe concernée se situe dans le rectangle rouge.
Elle est agrandie ci-dessous.
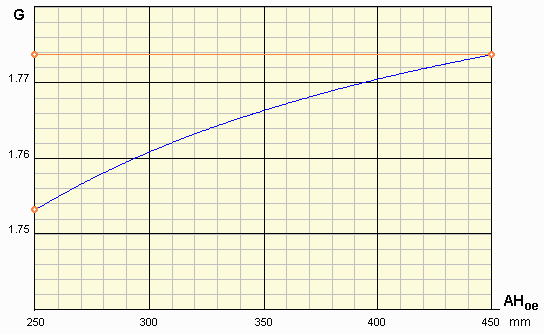
6) On constate :
- que le grossissement commercial Gc n'a rien à voir avec le grossissement réellement perçu par l'utilisateur de la loupe G :
dans le cas où x = 250 mm, aucune condition intrinsèque n'est respectée, et le grossissement réel est trois fois plus petit que le grossissement commercial !
- que le grossissement réel G varie avec la position de l'observateur :
il augmente* quand celui-ci s'éloigne, et tend vers le grandissement transversal de la loupe gy
(en effet, la distance objet-image devient alors négligeable par rapport à x et l'expression de G se réduit à celle de gy).
* L'augmentation est négligeable (de l'ordre de 1%) dans l'exemple ci-dessus.
- Lorsqu'une loupe donne d'un objet AB une image A'B', telle que AA' soit très petit par rapport à AHoe, distance objet-observateur, alors le grossissement de la loupe est voisin du grandissement transversal, et ne dépend donc plus de la position de l'observateur. C'est ici le cas : AA' = 6,67 mm << AHoe = 250 à 450 mm.
7) Appelons x la distance AS1 qui sépare l'objet du premier dioptre de la loupe.
Les positions des points cardinaux de la loupe, qui ont été translatés de x, seront notées F*, H*, H'* et F'* (voir schéma ci-dessous).
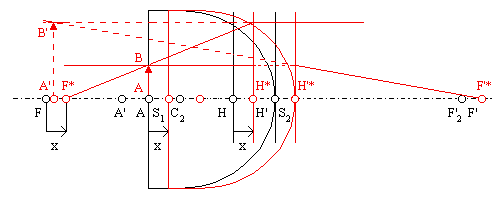La relation de grandissement de Newton, appliquée au couple (A, A'), donne :
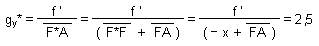
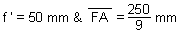
d'où l'équation du premier degré :
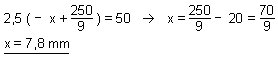
Le calcul de la position de l'image par la formule de Newton donne une distance de 125 mm entre le nouvel A' et F'*.
L'image A'B' est donc située 34 mm derrière AB.
(125 - (7,8 + 33,3 + 50) = 33,9 voisin de 34 mm)
Le grossissement sera proche de 2,5 si la distance observateur-objet est grande par rapport à 34 mm (cf. remarque 3 du 6).)
|