6. Observations et mesures de Galilée (1)

J.Hormière / février-mars 2002 Les observations de Galilée transcrites dans le Sidereus Nuncius peuvent être vérifiées avec les logiciels d'astronomie qui restituent, à une date et en un point de la terre donnés, la configuration des objets célestes. J'ai utilisé le logiciel anglais Redshift4 développé par Maris Technologies et édité en France par Alsyd Multimédia. Les images qui suivent sont des montages qui ont été réalisés à partir de copies d'écran. Les observations de Galilée Galilée rapporte 65 observations sur 46 jours répartis entre le 7 janvier et le 2 mars 1610 et effectuées de Padoue en Italie. J'ai choisi une dizaine d'exemples, afin de montrer la justesse, et de préciser les conditions optiques, de ses observations. La première observation (7 janvier 1610, à la première heure de la nuit) 1. Quelle heure était-il à la première heure de la nuit ? Environ 19h... Le 7 janvier 1610 à Padoue la lune se lève à 15h49 et le soleil se couche à 16h47. La pénombre se situe entre 16h55 et 18h35. Ces heures sont données en temps local. Pour obtenir le temps universel, il faudrait retrancher une heure. Les positions de la lune, du soleil et de Jupiter dans le ciel sont représentées sur les figures ci-dessous. 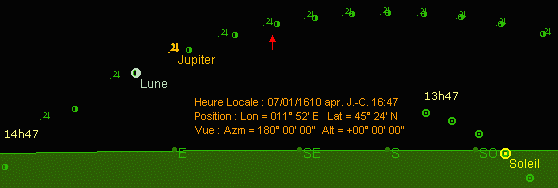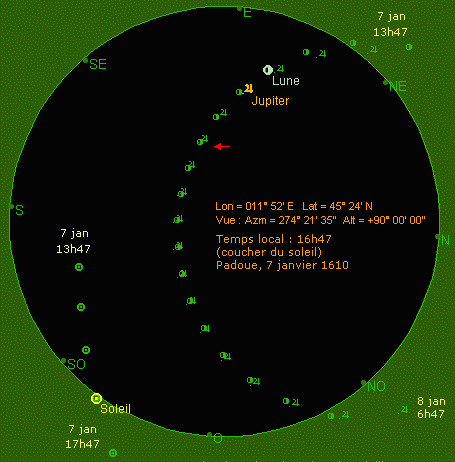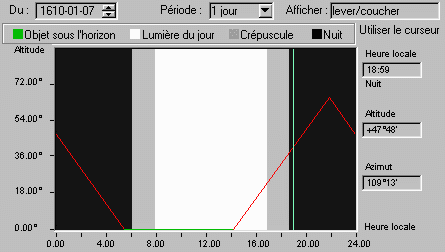La première représente ce que l'on voyait à l'horizontale quand on regardait plein Sud. La seconde représente la voute céleste telle qu'elle serait apparue si l'on avait regardé au zénith. La flèche rouge indique la position de Jupiter vers 19h. Jupiter vers 19h est située approximativement à mi-distance entre l'horizon et le zénith (voir figure ci-dessous). À 16h47, c'est le début de la pénombre. Jupiter, du fait de sa magnitude - 2,5, et de sa hauteur 20 °, est déjà discernable à l'œil nu. Lorsque la nuit va tomber le ciel sera bien éclairé par une lune presque pleine (phase 95% ; PL le 9 janvier). Supposons qu'à l'époque de Galilée la pénombre ne faisait pas partie de la nuit, et choisissons 19h comme heure d'observation. À ce moment là, la lune est dans la voie lactée ; Jupiter, en bordure, est à l'aplomb de la constellation d'Orion. La distance angulaire qui sépare la lune de Jupiter est de l'ordre de 12°. Galilée n'a donc aucune difficulté à diriger sa lunette vers la planète [1]. 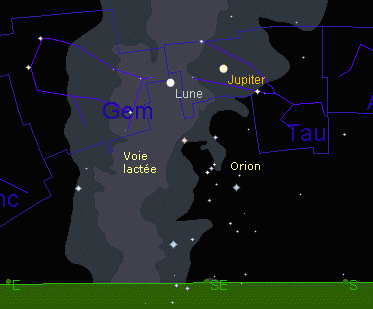Remarque : Comme le montre la figure suivante, la configuration de Jupiter et ses satellites ne change guère entre 17h47 et 19h47. Le choix de l'heure présumée d'observation supporte donc une large tolérance [2]. 2. Configuration géométrique Les trois satellites de Jupiter observables sont Callisto, Europe et Ganymède. Io est extrêment proche d'Europe (8"), ce qui n'est guère accessible à Galilée. (On verra plus loin qu'il arrive tout juste à distinguer avec sa lunette deux astres distants de 20".) On supposera - les deux satellites ayant à peu près la même magnitude - que c'est Europe, situé plus près (4,272 ua au lieu de 4,275 ua, où 1 ua représente une unité astronomique, c'est-à-dire 149 597 870 km = distance moyenne terre-soleil) qui a été observé (en réalité, c'est un mélange des deux satellites qui a été perçu). Les configurations entre la première heure qui suit le coucher du soleil (17h47) et la sixième heure (22h47) sont données ci-dessous. Les satellites sont représentés par des points exagérément grossis par le logiciel qui code ainsi leur magnitude. Dans la réalité de l'observation à la lunette, ce ne sont que des points, plus ou moins scintillants au gré des turbulences de l'atmosphère et très légèrement empâtés par les aberrations. 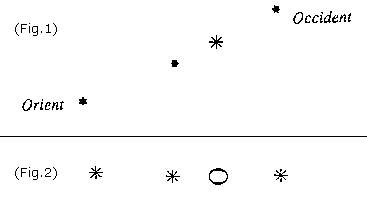Galilée donne deux représentations différentes (cf. Hallyn pages 71 et 143). La première est tirée d'une lettre rédigée le 7 janvier même. Elle fait apparaître une inclinaison correcte de la droite sur laquelle Jupiter et ses satellites sont quasi alignés. L'ordre de grandeur numérique que donne Galilée, « [la configuration] n'occupait pas plus qu'environ un degré en longitude » , est par contre erroné, et ce d'un facteur quatre, si l'on considère que la longitude est mesurée sur la direction que forme Jupiter avec ses satellites (direction voisine de l'écliptique). La seconde provient du Sidereus Nuncius. C'est une mise à plat, comme toutes les figures du livre se rapportant à Jupiter et ses planètes. Dans le graphique qui suit sont représentées les distances angulaires : 1 (Callisto-Europe), 2 (Europe-Jupiter) et 3 (Jupiter-Ganymède). Europe et Io sont distants de 8", La référence est donnée par le logiciel Redshift4, à 19h : C-IE : 7'8" IE-J : 2'9" J-G : 5'31" On tire de ces trois valeurs la distance angulaire qui sépare les satellites extrêmes : C-G : 14'48", soit environ ¼° On constate ainsi l'erreur d'un facteur 4 dans la première appréciation de Galilée. Les distances angulaires entre les satellites extrêmes des deux schémas de Galilée (Figures 1 et 2) sont ensuite estimées égales à cette valeur, et l'on en déduit les distances 1, 2 et 3. En ordonnées, les distances angulaires en minute d'arc. 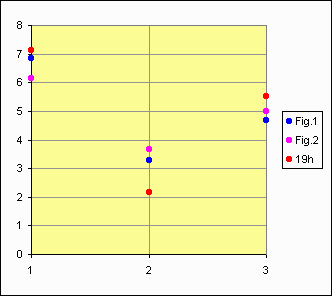Les erreurs sont de l'ordre de une minute d'arc. Nous verrons sur la page suivante que : d'une part Galilée ne représente les configurations qu'à peu près (au jugé), et d'autre part, que les valeurs numériques qu'il donne pour les distances angulaires séparant les astres ne sont pas tirées de ses propres schémas. 3. Photométrie des satellites de Jupiter Les satellites de Jupiter sont vus comme des points* à travers la lunette de Galilée, alors que Jupiter, de diamètre apparent 46", ramené à 14 ou 21 fois plus par le grossissement, soit une valeur comprise entre 11' et 16', est perçu comme un objet étendu. * Leurs diamètres apparents sont :       4,9 10-9 rad  →  Europe       5,7 10-9 rad  →  Io       7,5 10-9 rad  →  Callisto       8,2 10-9 rad  →  Ganymède Le plus grand, grossi d'un facteur 14, donne un angle de 0,26", loin d'être résolu par l'œil, car l'étendue est perçue à partir d'un angle supérieur à environ 1', soit 60". Les magnitudes des satellites sont données dans le tableau qui suit. Même si l'œil nu peut distinguer des objets célestes de magnitude inférieure à 6-7, et sur un ciel noir, les satellites ne pouvaient être perçus, bien que la distance qui séparait Callisto de Jupiter (supérieure à une dizaine de minutes d'arc) ait été parfaitement accessible (la résolution objet de la fovea est de l'ordre de une minute) et que leurs magnitudes respectives (6,14 / 5,48 / 4,81) aient appartenues au domaine du visible à l'œil nu. Les deux raisons de cette observation impossible étaient : le contraste de magnitude extrêmement important entre Jupiter et ses satellites ; Jupiter est 2,5127,33 = 855 fois plus lumineux que Ganymède et 2,5128,66 = 2910 fois plus lumineux que Callisto ; la luminance moyenne élevée du ciel, due à la presque pleine lune et à la voie lactée toute proche. Le gain de magnitude apporté par la lunette dépend de son facteur de transmission T et du rapport des aires de la pupille d'entrée de la lunette et de la pupille d'entrée de l'œil nu. En prenant T = 0,6 (minoration de T qui serait, avec une parfaite transparence des verres, de l'ordre de 0,964 = 0,85), et des pupilles de diamètres 26 mm et 5 mm, on obtient un gain de flux entrant dans l'œil de 0,6x(26/5)2 = 16,2 qui correspond en gros à un écart de magnitude de 3 (2,5123 = 15,9). Les magnitudes apparentes des satellites, de l'ordre de 2 à 3, sont parfaitement accessibles. Pour exemple, l'étoile polaire a une magnitude de 2, et zet Tau, située à 19h le 7/1/1610 à peu près au tiers de la distance lune-Jupiter, une magnitude de 3. 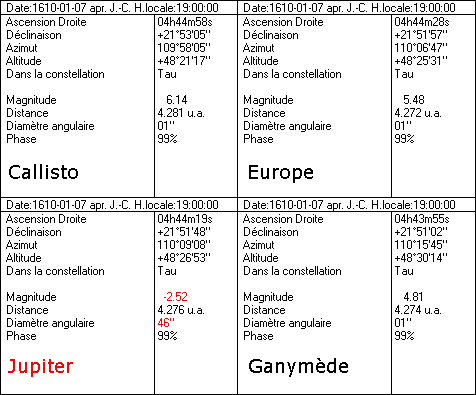[1] ??? : ??? ??? Le champ de la lunette de Galilée était assurément très petit : donner la valeur de la lunette russe que j'utilise. Mais quelqu'un de bien entraîné, observant les deux yeux ouverts (l'un regardant à travers la lunette et l'autre à l'extéreur), peut, en utilisant comme œil directeur l'œil nu, effectuer un pré-centrage, comme on le ferait aujourd'hui à l'aide de la lunette de visée associée en parallèle avec une lunette de fort grossissement. Les observations de Galilée n'ont donc eu rien de miraculeux. [2] Jean Meeus : Galileo's First Records of Jupiters's Satellites (Sky and Telescope, September 1962), p.137-139. Dans cet article, l'auteur calcule les positions des satellites de Jupiter du 7 au 15 janvier, et constate leur concordance avec les observations de Galilée. Il ne tient pas compte de la pénombre pour traduire en heure les indications de Galilée et fixe, par exemple, la première heure de la nuit le 7 janvier à 16h30 UT (temps universel), soit 17h30 heure locale. La différence de 1h30 avec l'heure que j'ai choisie (19h), n'a pas grande importance : les résultats sont quasiment les mêmes.