J.Hormière Errare humanum est, perseverare, diabolicum... en cas d'erreur, prévenez-moi s'il vous plaît : jo_hormiere@hotmail.com Le texte et les schémas sont propriétés exclusives de l'auteur Toutes reproductions interdites Exercice 1 1) Dans l'approximation de Gauss (ou approximation paraxiale) la distance focale image est le rapport de la taille y' de l'image d'un objet à l'infini, au diamètre apparent a de cet objet exprimé en radian, soit en reprenant les notations de l'énoncé : 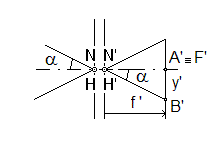 f ' = 2A'B'/2a = 20/0,04 à f ' = 500 mm 2) Comme l'objet est à l'infini, la première image se trouve dans le plan focal image de la première lentille, et la seconde, dans le plan focal image du doublet : ¥ → (L1) → A1 º F'1 → (L2) → A'º F' Calculs en valeurs algébriques... L'épaisseur du doublet est e =L1L2 = L1A' + A'L2 = 245 - 75 = 170 mm L2H' = L2F' + F'H' = L2F' - f ', soit, numériquement L2H' = 75 - 500 = - 425 mm Or la troisième formule de Gullstrand nous donne la position du point principal image H' : L2H' = - e f ' / f '1 On en déduit : f '1 = - e f '/L2H' = - 170 ×500/(-425) à f '1 = + 200 mm La première formule de Gullstrand nous permet de calculer la seconde distance focale : 1/f ' = 1/f '1 + 1/f '2 - e/(f '1f '2) 1/f ' = 1/f '1 + 1/f '2(1 - e/f '1) 1/1/f '2 = (1/f ' - 1/f '1)/(1 - e/f '1) = (1/500 - 1/200)/(1 - 170/200) d'où l'on tire f '2 = - 50 mm Remarque : Si l'on avait supposé l'image droite, on aurait trouvé : f ' = - 500 mm ; f '1 = + 147,826 mm et f '2 = + 17,114 mm. La seconde lentille serait convergente, ce qui est contradictoire avec l'énoncé : (L2) divergente... 1) La première chaîne d'images définie au I 1) reste valable. La première image se trouve donc dans le plan focal image de L1. Elle est renversée. La seconde image est dans le plan focal image du doublet. Le conjugué image de F '1 à travers L2 est simplement obtenu en appliquant une relation de conjugaison : par exemple, en valeurs algébriques, 1/L2F' = 1/L2F '1 + 1/f '2 = 1/(L2L1 + L1F '1) + 1/f '2 = 1/(- e + f '1) + 1/f '2 1/L2F' = 1/(- 140 + 200) + 1/(-50) = 1/60 - 1/50 = (5 - 6)/300 = - 1/300 L2F' = - 300 mm F'1 et F' étant de part et d'autre de L2, le grandissement transversal est négatif et y' est une image droite par rapport à l'objet à l'infini. 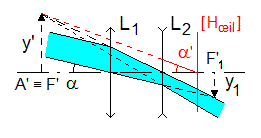 2) Le grossissement de la lunette est le rapport du diamètre apparent de l'image au diamètre apparent de l'objet vu à l'œil nu : G = a'/ a = (y'/A'Hœil)/a Comme par ailleurs y1 = f '1a et y'/y1 = gy (F'1, F') = L2F'/L2F'1, on obtient y' = y1 L2F'/L2F'1 = f '1a L2F'/L2F'1 en reportant dans l'expression de G, G = f '1 (L2F'/L2F'1)/A'Hœil A'Hœil = A'L2 + L2Hœil = 300 + 10 = 310 mm. G = 200 (300/60)/310 = 1000/310 à G = 3,2 Remarque : Une formule « toute faite » donne directement le grossissement, en valeur algébrique : G = Gi(1 - a/d) avec Gi : grossissement intrinsèque (- f '1/f '2) = - 200/(- 50) = 4 a = F'2Hœil = F'2L2 + L2Hœil = 50 + 10 = 60 mm d = A'Hœil = A'L2 + L2Hœil = 300 + 10 = 310 mm G = 4(1 - 60/310) = 4((310 - 60)/310) = 4 ×250/310 = 1000/310 = 3,2 3) 3.1 La pupille de sortie est le conjugué image du diaphragme d'ouverture à travers tous les composants optiques qui le suivent. Ici, la pupille de sortie Ps est le conjugué image de L1 à travers L2. 1/L2Ps = 1/L2L1 + 1/f '2 = 1/(-140) + 1/(- 50) = (- 5 - 14)/700 = - 19/700 L2Ps = - 700/19 à L2Ps = - 36,8 mm ØPs = ØL1 |L2Ps/L2L1| = 30 ((700/19)/140) = 150/19 à ØPs = 7,9 mm 3.2 Dans l'espace image, le faisceau utile associé au point image sur l'axe F', s'appuie sur la pupille de sortie Ps. Pour des points images situés en dehors de l'axe, le faisceau utile bascule et vient tangenter la lucarne de sortie Ls, à la limite du champ de pleine lumière PL' (voir schéma). 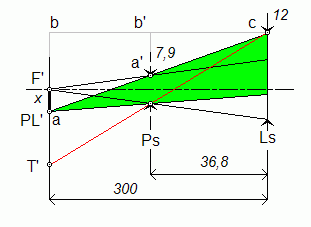 Des deux triangles semblables abc et a'b'c on tire : (6 - 3,95)/36,8 = (6 + x)/300 à x = 10,7 mm. Le diamètre du champ de pleine lumière dans l'espace image est ØPL' = 21,4 mm. 3.3 La distance focale image du doublet est obtenue à partir de : 1/f ' = 1/f '1 + 1/f '2 - e/(f '1f '2) = 1/200 - 1/50 + 140/(200×50) = - 1/1000 f ' = - 1000 mm. En tenant compte de la relation du I.1), le diamètre apparent du champ de pleine lumière objet est 2wPL = ØPL'/f ' = 21,4/1000 rad 2wPL = 0,0214 rad soit 1,23°. 3.4 Quand le point image s'écarte de l'axe optique au delà de la limite du champ de pleine lumière, la lucarne de sortie entame le faisceau qui s'appuie sur la pupille de sortie, jusqu'à le réduire, à la limite du champ total image T', à un seul rayon (cf. sur le schéma ci-dessus le rayon rouge). Le champ de contour est constitué par la couronne limitée par PL' et T'. Pour éliminer le champ de contour, il faut placer, dans le plan d'une image réelle, un diaphragme dont le diamètre est égal au diamètre du champ de pleine lumière à cet endroit-là. Comme les images F'1 et F' sont toutes deux virtuelles, on ne peut pas éliminer le champ de contour. 3.5 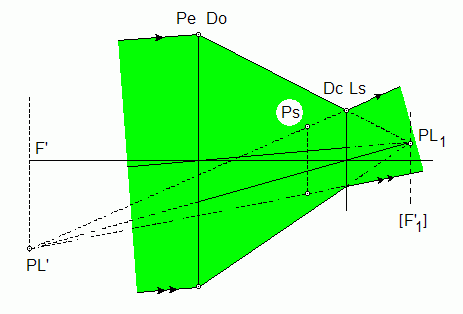 4) 4.1 Quand l'encombrement de la lunette (la distance qui sépare les deux lentilles) est égal à 150 mm, les foyers F'1 et F2 sont confondus et le système est afocal. 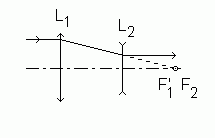 En effet, en valeurs algébriques, F'1F2 = F'1L1 + L1L2 + L2F2 = - f '1 + e + f2 F'1F2 = - 200 + 150 + 50 = 0 mm. 4.2 Le grossissement de la lunette est, en valeur absolue : G = |- f '1/f '2| = 200/50 à G = 4 Exercice 2 1) L'angle d'incidence r' sur le second dioptre est égal à l'angle A, c'est-à-dire à 30°. La loi de Descartes-Snell nous donne : no sinr' = sini'o et ne sinr' = sini'e Comme sinr' = sin30 = 0,5, sini'o = no/2 et sini'e = ne/2 On en déduit : i'o = 55,996 soit environ 56,0° i'e = 47,988 soit environ 48,0° 2) Di' = 56,0 - 48,0 = 8,0° 3) 4 L'indice du prisme est le rapport de la vitesse de la lumière dans le vide, à la vitesse de la lumière dans le milieu (vitesse et célérité sont synonymes). n = c/v donc v = c/n vo = c/no = 300 000 000/1,658 = 180 940 892 m.s-1 ve = c/ne = 300 000 000/1,486 = 201 884 253 m.s-1 5) Pour qu'il y ait émergence en I', l'angle d'incidence r' doit être inférieur ou égal à l'angle limite r'l. Cet angle limite est défini pour une émergence rasante, c'est-à-dire pour i' = 90°. no sini'lo = sin90 = 1 et ne sini'le = sin90 = 1 Donc i'lo = 37,095 soit environ 37,1° et i'le = 42,295 soit environ 42,3°. Si l'angle A du prisme varie continûment entre 30 et 45 degrés, il se produit d'abord, à partir de 37,1° une réflexion totale pour le rayon ordinaire (le rayon extraordinaire émerge alors seul du prisme par le dioptre AC), puis au delà de 42,3°, le rayon extraordinaire est lui aussi totalement réfléchi et plus aucun rayon n'émerge de AC. Retour au Menu |