Optique physique
pour le BTSOL

Exercices V


Joseph Hormière / Avril 2000

Corrigé des exercices de la première partie du livre
(édité chez Mediacom Vision en Septembre 1999)

clm.com@wanadoo.fr

Le texte et les schémas sont propriétés exclusives de l'auteur
Toutes reproductions interdites


Exercice 1
Exercice 2
Exercice 3
Exercice 4
Exercice 5
Exercice 6
Exercice 7
Exercice 8



1
1) Un polariseur parfait transmet 50% de la lumière naturelle qu'il reçoit.

Si l'intensité de la lumière naturelle incidente est I0, l'intensité à la sortie du premier polariseur est I = I0 / 2.

À la sortie du second polariseur, l'intensité I' est donnée par la loi de Malus :

I' = I.cos2a, où a est l'angle entre les deux polariseurs, soit I' = I0.cos2a / 2

Le facteur de transmission du système est T = I' / I0 = cos2a / 2.

a (°) 30 45 60 75
T (%) 37,5 25 12,5 3,35



2
1) Deux cas de figure se présentent : a et b (cf. schéma ci-dessous).

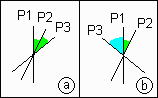
Polariseurs2
a.    I0, intensité incidente sur P1
      après P1, I1 = I0 / 2,
      après P2, I2 = I1 cos2a = I0 cos2a/ 2,
      après P3, I ' = I2 cos2a = I0 cos4a / 2

b.    I0, intensité incidente sur P1
      après P1, I1 = I0 / 2,
      après P2, I2 = I1 cos2a = I0 cos2a/ 2,
      après P3, I ' = I2 cos23a = I0 cos2a.cos23a / 2
Le facteur de transmission est T = I ' / I0

Cas de figure a : T = cos4a / 2

Le cosinus de l'angle est obtenu en prenant la racine quatrième de 2T, soit :

T 2T cosa a (°)
0,5 1 1 0
0,05 0,1 0,5623 55,78

Cas de figure b : T = cos2a.cos23a / 2

Le calcul est beaucoup plus compliqué. Il faut, dans un premier temps, exprimer cos3a en fonction de cosa :
cos3a = 4cos3a - 3cosa (voir calculs trigonométriques classiques).
En posant cos2a = x, on arrive à l'équation du second degré :
4 x2 - 3x - Ö(2T) = 0

T 2T cosa a (°)
0,5 1 1 et Ö(- 0,25) 0 et impossible
0,05 0,1 1,46 et Ö(- 1,38) impossible

2) Si les directions de P1 et P3 étaient parallèles, et si la direction de P2 était inchangée, on retrouverait les résultats du cas de figure a.
Toutefois, la direction de polarisation de la lumière émergente serait orientée comme P1, alors que dans le 1), elle était orientée à 2a de P1.

3) k + 1 polariseurs orientés de 5 en 5 degrés transmettent une intensité :
I' = I0 cos2k5 / 2
Avec un facteur de transmision T = 5%, on obtient :
cos2k5 / 2 = 0,05, soit cos2k5 = 0,1
En prenant le logarithme népérien de cette expression,
2k LN(cos5) = LN(0,1) ® k = 301,97
On arrondira à 302 pour être certain que le facteur de transmission est inférieur à 5%.


3
Pour que la lumière soit totalement polarisée en sortant de la cuve, elle doit s'être réfléchie sous l'angle de Brewster sur les dioptres eau-verre.

Soit i, r et i' les angles successifs que forme le rayon lumineux avec les normales aux dioptres air-eau et eau-verre.

Brewster

i' = i'B, tel que tani'B = nverre / neau = 3/2 / 4/3 = 9 / 8 = 1,125

On en déduit i'B = 48,3665°.

Comme les rayons incident et émergent forment un angle 2i, le trajet du rayon à travers le système admet comme axe de symétrie une normale au premier dioptre.
Le rayon réfléchi sur le premier dioptre eau-verre est parallèle au dioptre air-eau.
On en déduit A = 2 i'B = 2x48,3665
A = 96,73°

2i'B = 90 + r, donc r = 2i'B - 90 = A - 90 = 96,73 - 90 = 6,73°

La loi de Descartes-Snell appliquée au premier dioptre donne :
sini = (4 / 3) sinr = (4 / 3) sin 6,73 = 0,1563, d'où
i = 8,99° @ 9°


4
1) Le filtre doit être orienté de façon à ce que sa direction de polarisation soit horizontale (voir schéma ci-dessous).

Réflexion vitrine


Plus l'angle d'incidence i sur la vitrine est proche de l'angle de Brewster iB, et plus la lumière réfléchie sera polarisée rectiligne perpendiculairement au plan d'incidence (vecteur E).
Un polariseur rectiligne (P) dont la direction de polarisation sera contenue dans le plan d'incidence éteindra la lumière réfléchie.

De façon générale, le filtre polarisant atténuera le reflet.


5
Dans certains appareils photographiques reflex, le système de mesure de la lumière peut être sensible à la direction de polarisation de la lumière. Pour éviter que les mesures ne soient dépendantes de cette direction, et donc faussées, on utilise un filtre polarisant circulaire.

Polariseur circulaire

Ce filtre comprend un polariseur rectiligne associé à une lame quart-d'onde. La direction du polariseur rectiligne est à 45° des axes de la lame quart-d'onde. Les deux éléments restent solidaires l'un de l'autre.
Ce système permet :

6
1) Comme l'axe du cristal biréfringent est perpendiculaire au plan d'incidence, ce plan coupe les ondelettes centrées en I en trois cercles concentriques (voir schéma ci-dessous). Les rayons de ces cercles sont inversement proportionnels aux indices du premier milieu et du second milieu

Pour alléger le schéma, on a représenté uniquement les demi-cercles néceassaires aux constructions.

demi-cercle noir   : rayon K / 1 ;
demi-cercle bleu   : rayon K / no ;
demi-cercle rouge : rayon K / ne.

La construction de Huygens sur le premier dioptre consiste à :
  1. prolonger le rayon incident de 1 en 2 ;
  2. tracer la tangente au cercle en 2 et rechercher son intersection 3 avec le plan du dioptre ;
  3. tracer à partir de 3 les tangentes aux cercles qui correspondent aux ondelettes ordinaire et extraordinaire : les intersections sont 4 et 5 ;
    on utilise à cet effet le cercle dont le centre est le milieu de 13 et de rayon 13 / 2) ;
  4. joindre 1 aux deux points 4 et 5 pour obtenir les rayons réfractés ordinaire et extraordinaire.
La loi de Descartes-Snell découle de ces constructions :

sini = no.sinro    et    sini = ne.sinre

Sur le second dioptre, on construit les intersections des rayons ordinaire et extraordinaire : 6 et 7, puis l'on reprend pour chacun d'eux la construction de Huygens.

Rayon ordinaire        : 8, 9, 10
Rayon extraordinaire : 11, 12 et 13.

Prisme biréfringent

La loi de Descartes-Snell peut également être appliquée sur le second dioptre.

La réflexion totale du rayon ordinaire est obtenue lorsque les points 9 et 10 sont confondus.
L'angle d'émergence est égal à 90° et l'angle d'incidence est r'o, tel que :
no.sinr'o = 1xsin90 = 1

À partir des formules classiques du prisme :

sini = n.sinr
A = r + r'
sini' = n.sinr'

on obtient successivement :

r'o = 40,366 °
ro = 19,634 °
io = 31,25 °

Mêmes calculs pour la vibration extraordinaire :

r'e = 40,084 °
re = 19,916 °
ie = 31,94 °

2) Au minimum de déviation, la bissectrice de l'angle A est axe de symétrie pour le rayon qui traverse le prisme.

Les angles i et i' sont égaux, de même les angles r et r'.

A = 2r, donc r = A / 2 = 30°

sinie = 1,553 sin30 = 0,7765 ® ie = 50,94° = i'e

io = ie, sinre = sinio / 1,544 ® ro = 30,193°

r'o = A - ro = 60 - 30,193 = 29,807°

sini'o = 1,544 sinro = 1,544 sin 29,807 = 0,7675

i'o = 50,13°.

L'écart angulaire entre les deux rayons qui émergent du prisme est :
 (50,94 - 50,13) = 0,81°.


7
1) La lumière est polarisée circulaire à la sortie de la lame l / 4. L'intensité à la sortie de l'analyseur est indépendante de son orientation : I ' = Cte.
Voir cours page 82.

2) La différence de marche entre la vibration ordinaire et la vibration extraordinaire est : d = e.Dn = (2k + 1) l / 4, d'où
Dn = (2k + 1) l / (4e) = 0,6825 10-4(2k + 1)

k = 0 ® Dn = 0,68 10-4
k = 1 ® Dn = 2,05 10-4
k = 2 ® Dn = 3,41 10-4, etc.

3) Avec une épaisseur double, la lame devient « demi-onde » :

d = 2e.Dn = 2(2k + 1) l / 4 = (2k + 1) l / 2.

La lumière reste polarisée rectiligne à la sortie de la l / 2, et l'analyseur donnera, selon la loi de Malus, une intensité I ' variant sinusoïdalement avec l'angle qu'il forme avec la direction de polarisation de la vibration.

Plus précisément, la lame l / 2 transforme la vibration dont la direction de polarisation est orientée à 45° de ses axes en une vibration dont la direction de polarisation est symétrique de la précédente par rapport aux axes de la lame, c'est-à-dire en une vibration de direction de polarisation perpendiculaire.

En conséquence, il y aura extinction lorsque l'analyseur sera parallèle au polariseur, et maximum d'intensité quand il lui sera perpendiculaire.



8
1) Si l'analyseur éteint la lumière incidente, c'est que celle-ci est polarisée rectiligne, à 90° de la direction de polarisation de l'analyseur.

La lumière polarisée rectiligne qui a traversé la lame a conservé sa direction de polarisation.
Il y a donc trois possibilités :
  1. La lame est une lame « onde » orientée n'importe comment ;
  2. La lame est une lame « demi-onde » dont les axes sont parallèles au polariseur et à l'analyseur ;
  3. La lame est une lame « quart d'onde » dont les axes sont parallèles au polariseur et à l'analyseur.
2) Pour que l'extinction subsiste lorsque la lame tourne, la direction de polarisation de la vibration qui en émerge doit rester inchangée.

La seule solution possible est la lame « onde », car elle laisse inchangée une lumière polarisée rectiligne, quelle que soit son orientation.

3) Correctif à l'énoncé de la page 86 :

On remplacera dans l'énoncé 644 nm par 643 nm.

3.1
d = e.Dn = k.l
Le premier terme de l'équation est constant. k augmente quand l diminue. Les deux extinctions successives vérifient dont les équations :

e.Dn = k.l
e.Dn = (k + 1).l', d'où l'on tire :

k = e.Dn / l
k + 1 = Dn / l'

et par soustraction,

1 = e.Dn (1 / l' - 1 / l)

e = 1 / (Dn(1 / l - 1 / l')) = 1 / (0,009(1000 / 562,5 - 1000 / 600)) = 1000 mm
soit e = 1 mm.

3.2
k = e.Dn / l = 1000 x 0,009 / 0,6 = 15
On vérifie que pour k = 16, l = 0,5625 mm.

k = 17 ® l = 0,5294 m m (529,4 nm) .
k = 18 ® l = 0,5000 m m (500,0 nm).
k = 19 ® l = 0,4737 mm, qui se trouve en dehors du domaine de variation de la longueur d'onde.

page précédente à suivre...


DinOOptic

jo_hormiere@hotmail.com