Optique physique
pour le BTSOL

Exercices IV


Joseph Hormière / février 2000

Corrigé des exercices de la quatrième partie du livre
(édité chez Mediacom Vision en Septembre 1999)

clm.com@wanadoo.fr

Le texte et les schémas sont propriétés exclusives de l'auteur
Toutes reproductions interdites


Exercice 1
Exercice 2
Exercice 3
Exercice 4
Exercice 5
Exercice 6



1
1) On se reportera au cours, page 61.

d = a(sini' - sini), avec a, pas du réseau.

2) Pour que les interférences soient constructives, les rayons diffractés par chaque fente dans la direction i' doivent être en phase. La différence de marche, pour deux rayons consécutifs, doit être un multiple de la longueur d'onde :

d = k.l

3) 3.1 Lorsque i = 0°, d = a.sini' = k.l

Comme le sinus varie entre - 1 et + 1, k varie entre - a / l et + a / l

a = 1000/400 = 2,5 mm ; a / l = 2,5/0,48 = 5,2 ; - 5,2 < k < + 5,2

Les ordres de diffraction sont donnés par les valeurs entières de k, à savoir :

k = 0 ; ± 1 ; ± 2 ; ± 3 ; ± 4 ; ± 5 ;

3.2 Lorsque i = 90°, d = a.(sini'- 1) = k.l

Quand sini' = + 1, k = 0 ; sini' = - 1, k = - 2a / l = - 10,4

Les ordres diffractés sont obtenus pour :

k = 0 ; - 1 ; - 2 ; - 3 ; - 4 ; - 5 ; - 6 ; - 7 ; - 8 ; - 9 ; - 10

i = 0° i = 90°
k i'(°) k i'(°)
0 0 0 + 90
± 1 ± 11,07 - 1 + 53,90
± 2 ± 22,58 - 2 + 38,03
± 3 ± 35,17 - 3 + 25,09
± 4 ± 50,18 - 4 + 13,42
± 5 ± 73,74 - 5 + 2,29
- - - 6 - 8,74
- - - 7 - 20,12
- - - 8 - 32,41
- - - 9 - 46,72
- - - 10 - 66,93

4) 4.1 Déviation
La déviation est l'angle formé par :
le prolongement du rayon incident sur le réseau avec l'angle i,
et le rayon diffracté par le réseau dans la direction i'.

D = i' - i (cf schéma ci-contre)

Pour l'ordre 1, d = a.(sini' - sini) = l donne :
sini' = l / a + sini et D = Arcsin(l / a + sini) - i

Numériquement, D = Arcsin(0,2184 + sini) - i

4.2
Minimum de déviation


Courbe Calculatrice
D i D i
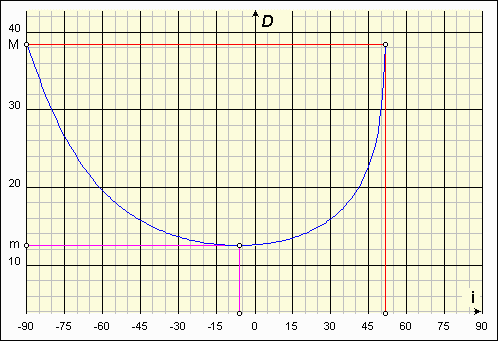
Maximum 38,5° 0° et 52° 38,59° 0° et 51,41°
Minimum 12,5° - 6° 12,54° - 6,27°


4.3 Remarque :

On rappelle les règles classiques de différentiation :

d(sinx) = cosx.dx ; d(Cte) = 0 ;
d(Cte.f(x)) = Cte.d[f(x)] ; d[(f(x) + g(x)] = d[f(x)] + d[g(x)]


Dans les équations (1) et (2) ci-dessous, k, a et l sont des constantes ;
les variables sont i (variable principale), i' et D.

a(sini' - sini) = kl (1) en différentiant, a(cosi'.di' - cosi.di) = 0 (1')
D = i' - i (2) en différentiant, dD = di' - di (2')

(2') ® dD / di = di' / di - 1

(1') ® cosi'.di' = cosi.di ® di' / di = cosi / cosi'

en reportant dans l'expression précédente, on obtient :

dD / di = cosi / cosi' - 1

Cette dérivée s'annule pour l'extremum, lorsque cosi = cosi'.

Dans le domaine de définition de ces angles [-90°, + 90°], il y a deux solutions :
i = i' et i = - i'
La première solution est à rejeter, car elle implique k = 0, or c'est dans l'ordre + 1 que le réseau est étudié.

On retient donc uniquement la seconde i = - i'

En conséquence, D = i' - i = i' - (- i') = 2 i' et
a(sini' - sin(-i')) = 2a.sini' = l ® sini' = l / 2a
L'application numérique conduit à :
i' = Arcsin(l / 2a) = Arcsin(0,546 / (2x2,5)) = 6,269°,
en reportant dans D : D = 2 i' = 2x6,269 = 12,538°.

En arrondissant à la deuxième décimale,

D(minimum) = 12,54° ; i' = 6,27° ; i = - 6,27°

4.4 sini' = l / a + sini

l = 400 nm (0,400 mm) ® i' = 2,91°
l = 750 nm (0,750 mm) ® i' = 11,00°
Di' = 11,00 - 2,91 ® Di' = 8,09°

Remarque :

Le calcul différentiel aurait donné :

a.cosi'.di' = dl, donne di' = dl / a.cosi'
L'angle i' est assez petit ; son cosinus, voisin de 1, varie peu avec la longueur d'onde ;
on peut l'approximer avec le cosinus de l'angle obtenu pour la radiation de référence (546 nm), c'est-à-dire avec cosi :
di' @ dl / a.cosi = 0,35 / (2,5xcos6,27) = 0,141 rad, soit 8,08°.

On trouve, par cette méthode approximative, un résultat très voisin de celui calculé précisément au dessus.

2
1) Le faisceau parallèle qui éclaire la fente est obtenu en décentrant une source ponctuelle collimatée (voir schéma ci-dessous).

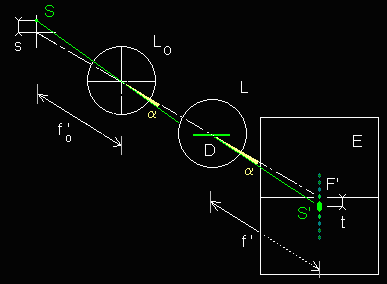
Diffraction par une fente


La figure de diffraction (diffraction de Fraunhofer ou diffraction à l'infini) est observée au voisinage de l'image géométrique S' de la source S.
Elle est constituée d'une tache très brillante, décentrée par rapport au foyer principal image F' de L d'une quantité t = - s f ' / f '0.
Cette tache est symétriquement entourée de taches alternativement sombres et brillantes disposées sur une droite passant par F' orthogonale à la fente.
L'intensité des taches brillantes décroît très rapidement.
La tache centrale est deux fois plus large que les autres taches brillantes.

2) Position du centre de la tache de diffraction
Comme il a été précisé plus haut, le centre de la tache de diffraction est confondu avec l'image géométrique de la source S.
Il est décalé de t = - s f ' / f '0 par rapport à F'.

Le faisceau éclairant la fente est incliné de 20°, donc s / f '0 = tan20° = 0,364.
0,364 x f ' = 0,364 x 250 = 90,99 mm
Le centre de la figure de diffraction est décentré d'environ 91 mm.

Largeur de la tache centrale :
L'intensité relative diffractée par la fente est de la forme :

I / Imax = (sinu / u)2, avec u(rad) = pd (sina' - sina) / l

a : angle d'incidence du faisceau éclairant la fente,
a' : angle de diffraction.

Intensité diffrcatée


Les zéros de la fonction correspondent aux minimums d'intensité.
Ils s'obtiennent en écrivant sinu = 0 (u ¹ 0).
u(rad) = kp (k ¹ 0), soit k = ..., - 2, - 1, + 1, + 2,...
sina' = a + k.l / d.

Une fois calculés les angles a' correspondant aux minimums d'intensité, les positions sur l'écran s'obtiennent an calculanbt f '.tana' (voir tableau ci-dessous).

k sina' a' (°) f '.tana'
- 2 0,3320 19,3914 87,9969
- 1 0,3370 19,6954 89,4905
+ 1 0,3470 20,3052 92,5034
+ 2 0,3520 20,6109 94,0232


La largeur du maximum central est : 92,5034 - 89,4905 = 3,0129, soit environ 3 mm. Distance séparant les minimums d'intensité :
La distance séparant les minimums d'intensité est :
89,4905 - 87,9969 = 1,4936 mm ;
94,0232 - 92,5034 = 1,5198 mm.
soit environ 1,5 mm.

Remarque :

La largeur de la tache centrale de diffraction est inversement proportionnelle à cos3a (voir schéma ci-dessous).

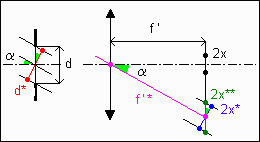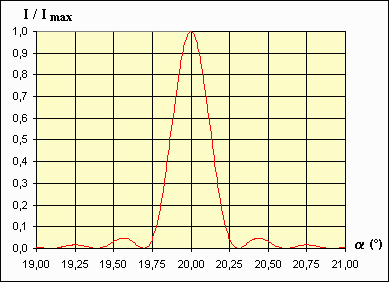
cosinus-cube La largeur de la tache centrale est :

2x** = 2x* / cosa, avec
2x* = 2lf '* / d*, soit
2x** = 2lf '/d.cos3a
2x** = 2x / cos3a

2x = 2lf ' / d = 2x500x250 / 100 000 = 2,5 mm.
2x** = 2x / cos3a = 2,5 / cos320 = 3,0129 mm, ce qui correspond bien à la valeur calculée plus haut à partir des résultats du tableau.

3) L'image S' de S ne change pas quand la fente est tournée, translatée ou diminuée.
La figure de diffraction reste donc centrée en S'.



3

L'énoncé est incomplet !!! (mea maxima culpa)

Il fallait lire :

Un détecteur supposé ponctuel est placé dans un plan situé à une distance L = 2 m du fil...
le détecteur coïncide avec le dixième minimum d'intensité de la figure de diffraction défini à partir du centre de celle-ci (la distance qui les sépare est égale à 255 mm).

 1) Le minimum d'ordre k se trouve dans la direction q, telle que sinq = k.l / dN

De plus tanq = x / L.

On en déduit : dN = kl / sinq = kl / sin(Arctan(x / L))

dN = 10x633x10-6 / sin(Arctan(255 / 2000)) ® dN = 0,050 mm (soit 1 / 20 mm)

Diffraction par un fil


2) Quand la figure de diffraction se dilate, le diamètre du fil diminue.

Cela est du au fait que les positions des minimums d'intensité sont inversement proportionnelles au diamètre (ou à la largeur) d du fil.

3) La formule du 1) reste valable. d / k reste constant. :

dN / 10 = d / k ® d = k dN / 10

k = 9 ® d = 9x0,050/10 ; d = 0,045 mm

k = 11 ® d = 11x0,050/10 ; d = 0,055 mm

Le domaine de variation de d est : [0,045 mm ; 0,055 mm]


4
1) L'expression de la différence de marche est (cf. cours page 61) :

d = a(sini' + sini) = kl

i = 30° et a = 4 mm   ®  4(sini' + 0,5) = kl

sini' = + 1   ®   + 6 = kl   ®   k = + 6 / l
sini' = - 1   ®   - 2 = kl   ®   k = - 2 / l

l = 380 nm

- 5,26 < k < + 15,79
21 ordres observables (de - 5 à +15, 0 compris)

l = 780 nm

- 2,56 < k < + 7,69
10 ordres observables (de - 2 à + 7, 0 compris)

k 380 780 k 380 780
- 5 - 77,16 - + 6 + 4,01 + 42,07
- 4 - 61,64 - + 7 + 9,50 + 59,88
- 3 - 51,72 - + 8 + 15,07 -
- 2 - 43,63 - 62,87 + 9 + 20,79 -
- 1 - 36,51 - 44,03 + 10 + 26,74 -
0 - 30 - 30 + 11 + 33,03 -
+ 1 - 23,89 - 17,76 + 12 + 39,79 -
+ 2 - 18,06 - 6,32 + 13 + 47,31 -
+ 3 - 12,42 + 4,88 + 14 + 56,10 -
+ 4 - 6,89 + 16,26 + 15 + 67,67 -
+ 5 - 1,43 + 28,36 - - -


2) Compte-tenu des conventions de signe, la direction faisant un angle de 90° avec le faisceau incident correspond à un angle i' = - 60°.

La différence de marche devient :

d = a(sin(- 60) + sin30) = 4(- Ö3 / 2 + 1 / 2) = 2(1 - Ö3) = kl

l = 380 nm   ®   k = 2(1 - Ö3) / 0,38 = - 3,85
l = 780 nm   ®   k = 2(1 - Ö3) / 0,78 = - 1,88

Les solutions sont les valeurs entières de k comprises entre les deux bornes précédentes : k = - 2 et k = - 3.

k = - 2   ®   l = 732 nm
k = - 3   ®   l = 488 nm


5
1) Remplaçons dans le nombre d'Abbe par sa valeur numérique et (nF' - nC') par leurs expressions en fonction de b et l :

ne = (ne - 1)/(nF' - nC') = (1,525 - 1) / (a + b / 4802 - a - b / 6442)
59 = 0,525 / (b (1 / 4802 - 1 / 6442) = 272 147 / b
ce qui donne, b = 272 147 / 59 ; b = 4 613 nm-2

ne = 1,525 = a + b / 5462 = a + 4 613 / 5462
a = 1,525 - 4 613 / 5462 ; a = 1,5095

nF' = 1,5095 + 4 613 / 4802 = 1,5295      nF' = 1,530
nC' = 1,5095 + 4 613 / 6442 = 1,5206      nC' = 1,521

3) Au minimum dedéviation, la bissectrice de l'angle A est axe de symétrie pour le rayon qui traverse le prisme. Les angles d'incidence sur le premier dioptre et de réfraction sur le second sont égaux (i = i'), de même les angles de réfraction sur le premier dioptre et d'incidence sur le second (r = r').

Rappelons les quatre formules du prisme :

  1. sini = n.sinr
  2. sini' = n.sinr'
  3. A = r + r'
  4. D = i + i' - A
Au minimum de déviation r = r' = A / 2 = 60 / 2 = 30°

sinime = ne.sin30 = 1,525x0,5 = 0,7625  ®   ime = 49,69°

Dme = 2ime - A = 2x49,69 - 60  ®   Dme = 39,38°

4) L'application des formules du prisme aux radiations bleue et rouge donne :

l = 480 nm  ®   r = 29,89° ; r' = 30,11° ; i' = 50,13° ; D = 39,82°
l = 644 nm  ®   r = 30,09° ; r' = 29,91° ; i' = 49,33° ; D = 39,02°

Les valeurs du tableau de la page 63 sont calculées avec le maximum de précision que permet une calculatrice. Ici les arrondis introduisent des erreurs relativement faibles :

(39,82 - 39,78) / 39,78 @ (39,02 - 38,99) / 38,99 @ 0,1% !

5) Dans le cas d'une incidence normale, la déviation d'un faisceau est égale à l'angle i'.

d = a.sini' = l
D = i' = Arcsin(l / a

l = 480 nm  ®  D = Arcsin(0,48 / 2) ; D = 13,89°
l = 644 nm  ®  D = Arcsin(0,644 / 2) ; D = 18,78°

Ces résultats correspondent effectivement à ceux donnés dans le tableau de la page 63.

6) En utilisant les valeurs précédemment calculées,

dD / dl = - 2b sinA / (l3 cosr cosi') devient pour

l = 480 nm : dD / dl = - 2x4613 sin60 / (4803 cos29,89 cos50,13)
dD / dl = - 1,2999 10-4 rad.nm-1, soit en valeur absolue 7,45 °.mm-1

l = 644 nm : dD / dl = - 2x4613 sin60 / (6443 cos30,09 cos49,33)
dD / dl = - 5,3052 10-5 rad.nm-1, soit en valeur absolue 3,04 °.mm-1

Ces résultats correspondent, à moins de 0,5% près, à ceux donnés dans le tableau de la page 63 (7,42 et 3,03).

Dans le cas du réseau, la formule qui donne le pouvoir dispersif est :

di'/ dl = dD / dl = k a.cosi' = 1 / 2 cosi'

l = 480 nm : dD / dl = 1 / 2 cos13,89
dD / dl = 5,1506 10-1 rad.mm-1, soit 29,51 °.mm-1

l = 644 nm : dD / dl = 1 / 2 cos18,75
dD / dl = 5,2802 10-1 rad.mm-1, soit 30,25 °.mm-1

Ces résultats correspondent presque exactement, à ceux donnés dans le tableau de la page 63 (29,51 et 30,26).

Remarques :

Les résultats de signe opposé pour le pouvoir dispersif du prisme et du réseau traduisent le fait que : pour un prisme, le bleu est plus dévié que le rouge, alors que pour un réseau, c'est le rouge qui est plus dévié que le bleu.

Le prisme est plus dispersif dans le bleu que dans le rouge. Dans le cas du réseau c'est l'opposé.

Le pouvoir dispersif du réseau est nettement plus important que celui du prisme.
Il pourrait être augmenté pour le prisme de deux façons :
 7) Les déviations ont été calculées au 4) et 5).

Prisme : DD / Dl = (39,82 - 39,02) / (0,644 - 0,480) = 0,8 / 0,164
DD / Dl = 4,88°.mm-1

Réseau : DD / Dl = (18,78 - 13,89) / (0,644 - 0,480) = 4,89 / 0,164
DD / Dl = 29,82°.mm-1


6
1)

Appareil photographique :

On assimile l'objectif à une lentille mince convergente diaphragmée sur elle-même.

Le rayon de la tache d'Airy dans le plan focal image de l'objectif est :

r = 1,22lf ' / ÆPs ; or ÆPs = ÆPe = f ' / N, donc

r = 1,22lN = 1,22x0,555x5,6 = 3,79 mm.

Le rayon de la tache d'Airy est plus petit que le grain : c'est donc ce dernier qui limite le pouvoir séparateur de système photographique.

Lunette astronomique :

La formule précédente reste valable.

r = 1,22lN = 1,22x0,555x8 = 5,42 mm.

Microscope :

Le diaphragme d'ouverture est dans l'espace intermédiaire du microscope.
Comme la distance D qui sépare ce diaphragme du plan image intermédiaire (intervalle optique) est grande par rapport au diamètre du diaphragme Do (1,41 << 160) , il est possible de raisonner en terme de diffraction à l'infini.

Le rayon de la tache d'Airy est :

r = 1,22lD / ÆDo

La relation d'Abbe (ou relation des sinus, ou relation d'aplanétisme) s'écrit :

n.y.sinu = y1.sinu1, et comme u1 est petit, sinu1 @ tanu1 = ÆDo / 2D.

n.sinu est l'ouverture numérique de l'objectif (ON).
y1 / y est, en valeur absolue, le grandissement de l'objectif (|gyob|) ; il s'en suit que :

ÆDo = 2 D.ON / |gyob| = 2x160x0,65 / 40 = 5,20 mm

En reportant dans l'expression du rayon de la tache d'Airy,

r = 1,22x0,555x160 / 5,20 = 20,83 mm.

Oeil emmétrope :

Le diamètre de la pupille de sortie est : ÆPs = gypupÆPe = 0,92x3 = 2,76 mm.

r = 1,22l.PsR' / nÆPs = 1,22x0,555x20,52 / (1,336x2,76) = 3,77 mm.

2) Le calcul du conjugué objet du rayon de la tache d'Airy fait intervenir une relation image/objet : la focale image de l'objectif, dans les deux premiers cas, le grandissement de l'objectif dans le troisième, et la distance focale objet de l'oeil dans le quatrième.

qdiff = r / f '

Appareil photographique :

qdiff = 3,79 / 50 000 = 7,58 10-5 rad, soit 15,6".

Lunette astronomique :

qdiff = 5,42 / 400 000 = 1,36 10-5 rad, soit 2,8".

Microscope :

ydiff = r / |gyob| = 20,83 / 40 = 0,52 mm.

Oeil emmétrope :

Doe = - 1 / foe  ®  |foe| = 1000 / 60 = 16,67 mm.

qdiff = r / |foe| = 3,77 / 16 670 = 2,26 10-4 rad, soit 47".

3) La limite de séparation objet due au détecteur se calcule à partir d'une relation image/objet : la focale de l'objectif pour le premier cas, le grossissement pour le second, la puissance intrinsèque pour le troisième, et la focale objet pour le quatrième.

Appareil photographique :

qdét = g / f ' = 5 / 50 000 = 10-4 rad soit 20,6".

Lunette astronomique :

Le grossissement de la lunette afocale est égal au rapport de la focale de l'objectif à la focale de l'oculaire, soit 400 / 25 = 16.

qdét = LSoeil / G = 1,2' / 16 = 1,2x60 / 16 = 4,5".

Microscope :

La puissance intrinsèquedu microscope est égale au produit du grandissement de l'objectif par la puissance intrinsèque de l'oculaire, c'est-à-dire le quart de son grossissement commercial :
Pi = gyob.Pioc = gyob.Gcoc / 4 = 40x10/4 = 100 dioptries.

ydét = tan(LSoeil) / Pi = tan(1,2')/100 = 3,49 10-6 m, soit 3,49 mm.

Oeil emmétrope :

La valeur est donnée dans l'énoncé : 1'12"

En RÉSUMÉ,

LSdiff LSdét
Appareil photographique 15,6" 20,6"
Lunette astronomique 2,8" 4,5"
Microscope 0,52 mm 3,49 mm
Oeil emmétrope 47" 1' 12"

On constate, dans les exemples choisis,
que c'est le détecteur qui limite les performances du système optique.


page précédente à suivre... page suivante


DinOOptic

jo_hormiere@hotmail.com