Optique physique
pour le BTSOL
Exercices III
Joseph Hormière / Décembre 1999
Corrigé des exercices de la troisième partie du livre
(édité chez Mediacom Vision en Septembre 1999)
clm.com@wanadoo.fr
Le texte et les schémas sont propriétés exclusives de l'auteur
Toutes reproductions interdites
Exercice 1
Exercice 2
Exercice 3
Exercice 4
Exercice 5
1
A
1) On adaptera le schéma de la page 37 du cours
(cas particulier d'un coin de verre, avec le rayon incident est perpendiculaire au premier dioptre) :
Le rayon 1' reste inchangé après traversée de la première lame de verre.
Le rayon JM conserve sa direction, mais il est décalé transversalement vers la gauche, après traversée de la lame.
Le plan de localisation des interférences (en pointillés sur le schéma) est translaté dans une direction normale à la première lame de verre de e(n - 1)/n (e, n : indice de réfraction et épaisseur de la lame de verre).
Solution simplifiée :
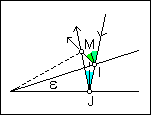On néglige l'épaisseur e de la lame de verre, d'où le schéma ci-contre.
Le rayon incident se dédouble en I.
Les deux rayons réfléchis IM et JM
se coupent en M où ils interfèrent.
2) Les franges sont localisées au voisinage de la lame d'air.
C'est « l'expression consacrée », car l'épaisseur d'air est extrêmement petite,
et la position exacte du plan de localisation, à quelques micromètres près, importe peu.
3) On se reportera à la page 38 du cours.
La démonstration sera adaptée au coin d'air, en remplaçant n par 1.
On obtient : i = l / (2e), avec e en radian.
4) Les deux coins d'air formés I et II ont le même angle e ; ils donnent donc le même interfrange i.
Par réflexion, on observe sur l'arête du coin d'air une frange sombre.
En effet, en incidence normale ou proche de la normale, la différence de marche est :
d = 2e + l / 2
et pour e = 0, d = l / 2, ce qui correspond à un déphasage de p radian entre les vibration qui interfèrent, et donc à une opposition de phase pour les vibrations qui interfèrent.
Le décalage des deux systèmes de franges est égal au décalage des deux franges sur l'arête des coins d'air.
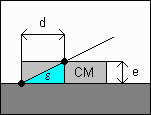Le schéma ci-contre représente une section droite des coins d'air (CM : couche mince).
Dans le triangle bleu, tane = erad = e / d
soit e = d.erad
5)
En explicitant e dans la formule de l'interfrange (voir question 3.), on obtient :
e = l / (2i)
d'où e = dl /(2i) (C.Q.F.D.)
6) Application numérique :
Comme l'épaisseur de la couche mince est inférieure à une demi-longueur d'onde, le décalage d est inférieur à l'interfrange i (voir formule précédente).
Sur la Figure 2 de l'énoncé,
d = x2 - x1 = 3,04 - 2,54 = 0,50 mm
i = (x3 - x2) / 3 = (9,49 - 3,04) / 3 = 6,45 / 3 = 2,15 mm
d'où e = (0,50 / 2,15)x(l / 2) = 0,233 x(l / 2) = 63,5 nm
B 1) En lumière blanche on observe, au voisinage de l'arête du coin d'air, des teintes de Newton (teintes à centre noir).
Ces teintes sont disposées symétriquement par rapport à la frange noire.
Très saturées au voisinage de la frange, elles se délavent de plus en plus pour donner, à partir d'une certaine distance, du blanc d'ordre supérieur.
Dans le champ observé, le décalage entre les deux systèmes d'interférence est donné par la distance qui sépare les deux franges noires.
Si ce décalage était plus grand que la largeur du champ, alors il faudrait augmenter l'angle e du coin d'air afin de diminuer l'interfrange.
2) Il n'est pas possible d'observer des franges d'interférence d'ordre élevé, car les franges produites par chacune des radiation visible du spectre de la lumière blanche sont décalées les unes par rapport aux autres et l'addition de leur intensités donne du blanc.
3) L'intersection du plan définissant les coins d'air et la pente de la couche donne un segment.
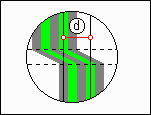Les franges de même ordre des deux systèmes seront donc reliées entre elles par un segment de frange.
Cela permettra de repérer le décalage d, quelque soit la valeur de e, et ainsi de pouvoir travailler en lumière monochromatique.
2
1) Voir question 3. du précédent exercice.
i = l /(2e)
Une minute d'angle correspond à un soixantième de degré, et un degré, à p/180 radian.
10' correspond donc à 10 p / (180x60) = 2,909 10-3 rad.
i = 500 / (2x2,909 10-3) = 85944 nm, soit i = 86 mmm
2) L'interfrange est proportionnel à la longueur d'onde. Si celle-ci augmente, il augmente aussi.
3) Sur l'arête du coin d'air l'ordre d'interférence est nul ou égal à 1/2 selon que les interférences sont observées en transmission ou en réflexion.
Deux franges de même nature, dues aux deux radiations, coïncident.
8,6 millimètres représentent 100 interfranges pour la radiation de longueur d'onde l.
La première coïncidence se produit lorsque 100 i = k' i', où k' est un nombre premier avec 100 (voir remarque ci-dessous) et inférieur à celui-ci.
Comme 100 = 2x2x5x5, les multiples de 2 et de 5 inférieurs à 100 ne conviennent pas. Les premières valeurs possibles sont : 99, 97, 93, ...
100 i = k' i', soit 100 l / (2e) = k' (l + Dl) / (2e)
soit
Dl = l / k'
On obtient les résultats suivants :
| k' |
99 |
97 |
93 |
| Dl en nm |
5,05 |
5,15 |
5,38 |
Remarque :
Deux nombres sont premiers entre eux si leur seul divisieur commun est 1 :
par exemple, 25 et 18 (25 = 1x5x5 ; 18 = 1x2x3x3)
3
Un viseur à frontale fixe est équivalent à un microscope de faible grossissement.
Il est utilisé sur banc d'optique pour effectuer :
- des pointés longitudinaux (pour mesurer la focale d'une lentille mince, par exemple),
- des pointés transversaux (c'est le cas ici).
1) Dans le plan des interférences l'interfrange varie entre 1/40 mm et 10/4 mm, c'est-à-dire 25 mm et 2500 mm.
La formule de l'interfrange donne erad = l / 2i.
Les résultats sont regroupés dans le tableau ci-dessous.
| e |
i' = 1/10 mm |
i' = 1 cm |
| radian |
0,0116 |
0,000116 |
| degré |
0,665 |
0,00665 |
| ° ' " |
40' |
24" |
2) Pour la formation des interférences, on se reportera à l'exercice 1.
4
Considérons un anneau d'ordre p (p, entier s'il est brillant ; p, demi-entier, s'il est sombre).
La différence de marche, pour une incidence normale ou proche de la normale est :
d = 2e + l / 2 = p.l
L'épaisseur d'air, à une distance x du centre des anneaux, est approximativement égale à :
x2 / 2R.
En reportant dans l'expression de la différence de marche,
d = x2 / R + l / 2 = p.l
Cela donne :
x2 = (p - 0,5)lR (1)
Si l'on introduit un liquide d'indice n dans la lame d'air, l'indice de la lame interférentielle passe de 1 à n.
Dans l'expression de la différence de marche, il faut remplacer e par ne, ou bien, dans la formule (1), R par R / n.
x'2 = (p - 0,5)lR / n = x2 / n (1)
Si p, l et R sont fixés, x' est nécessairement plus petit que x, car n est supérieur à 1.
On retiendra que : lorsque la lame d'air est remplacée par une lame liquide, toutes choses égales par ailleurs, les anneaux se resserrent.
Ecrivons que, là où le diamètre du troisième anneau du à la lame d'air est égal au diamètre du quatrième anneau du à la lame de liquide, l'ordre d'interférence diffère de une unité :
x2 / R = (p - 0,5)l
n.x2 / R = (p + 0,5)l
Cela donne, en divisant la deuxième équation par la première,
n = (p + 0,5) / (p - 0,5)
En supposant - ce qui n'est pas vraiment explicite dans l'énoncé, mais que l'on peut déduire de la figure - que ce sont les troisième et quatrième anneaux sombres qui ont le même diamètre, l'ordre p est égal à 3,5.
d'où n = 4 / 3 = 1,33
5
Lors de la contrainte la surface convexe s'applatit et son rayon de courbure augmente.
Les franges d'égale épaisseur représentent les lignes de niveau de la lame d'air (cf. cours page 42).
Elles sont obtenues, pour les franges sombres, en recherchant les intersections avec le dioptre sphérique des surfaces déduites de la surface du dioptre plan de contact, par translation de k.l / 2.
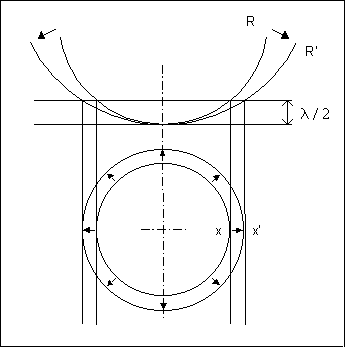
Dans l'exemple ci-dessous, le rayon de courbue R devient égal, après contrainte, à R' (R' > R) ,
et le rayon du premier anneau sombre de diamètre non nul x devient égal à x' (x' > x).
Le raisonnement peut être généralisé à tout anneau.
Une autre façon de raisonner consisterait à partir de la formule de la différence de marche qui permet de calculer le rayon de l'anneau d'ordre p en fonction de R et l :
x2 / R = (p - 0,5)l
Si R augmente, p et l restant constants, x augmente nécessairement.
D'où la conclusion : la contrainte qui déforme la lentille et augmente le rayon de courbure du rayon convexe induit une augmentation du diamètre des anneaux de Newton.
 |
à suivre... |
 |
DinOOptic
