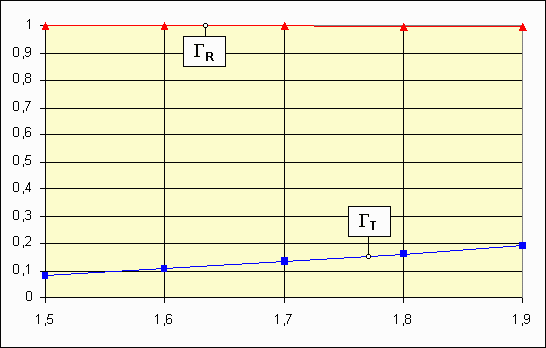
Variation du contraste des anneaux d'égale inclinaison en fonction :
de l'indice de la lame de verre, et de l'observation.
 IKM représente le trajet de la lumière dans le verre.
IKM représente le trajet de la lumière dans le verre.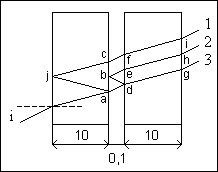
| en transmission | G = 2R / (1 + R)2 | |
| en réflexion | G = 2T / (1 + T)2 |
| GT | GR | |
| 1,5 | 0,080 | 0,999 |
| 1,6 | 0,106 | 0,999 |
| 1,7 | 0,134 | 0,998 |
| 1,8 | 0,162 | 0,996 |
| 1,9 | 0,191 | 0,995 |

| au centre | do = 2e + l / 2 = po.l | |
| au bord | d = 2e.cosi + l / 2 = (po - 4).l | |
| do - d = 2e(1 - cosi) = 4l |
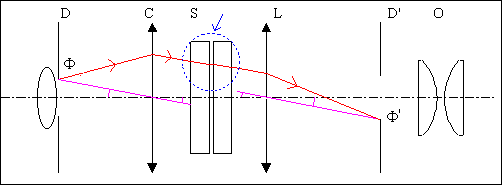

| p | i° | i'° | 2i'° |
| 5493 | 1,34 | 7,73 | 15,45 soit 15° 27' 6" |
| 5492 | 1,73 | 9,97 | 19,93 soit 19° 56' 2" |
| l nm | ||
| p | Transmission | Réflexion |
| 64,5 | 480,6 | 484,4 |
| 63,5 | 488,2 | 492,1 |
| 62,5 | 496,0 | 500,0 |
| 61,5 | 504,1 | 508,2 |
| 60,5 | 512,4 | 516,7 |
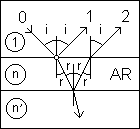 1) Un rayon (0) qui arrive sur la couche antireflet est partiellement réfléchi suivant (1).
1) Un rayon (0) qui arrive sur la couche antireflet est partiellement réfléchi suivant (1). | i ° | 0 | 30 | 45 | 60 |
| r ° | 0,00 | 21,24 | 30,82 | 38,87 |
| r' ° | 0,00 | 18,21 | 26,23 | 32,77 |
| r | 0,160 | 0,163 | 0,184 | 0,261 |
| r' | 0,074 | 0,074 | 0,077 | 0,083 |
| T | 0,975 | 0,973 | 0,966 | 0,932 |
| R % | 0,77 | 0,88 | 1,47 | 4,33 |
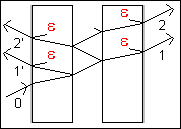 Le traitement antireflet sur les dioptres externes des lames de verre
Le traitement antireflet sur les dioptres externes des lames de verre | à suivre... | |