1. Doublet de Ramsden
Un doublet de lentilles minces (L1, L2) a pour symbole 3-2-3, et pour épaisseur 12 mm.
1) Déterminer par le calcul sa distance focale f ' et la position de ses points cardinaux.
On donnera, en valeur algébrique, O1H, O1F, O2H' et O2F'
2) Vérifier les résultats sur un schéma à l'échelle 2.
Le doublet a pour symbole (ou pour formule) 3-2-3.
On en déduit :
f '1 = 3a = f '2 et e = 2a
e = 2a = 12 mm, donc a = 6 mm, f '1 = f '2 = 18 mm
Comme il est symétrique (milieux extrêmes identiques et f '1 = f '2), les points cardinaux-image sont symétriques des points cardinaux-objet par rapport au milieu du doublet. Il suffit donc de déterminer les points cardinaux-image ; les points-objet s'en déduisent ensuite par une simple symétrie.
1) 1ère solution (méthode des foyers) :
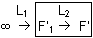
Relation de conjugaison de Descartes :
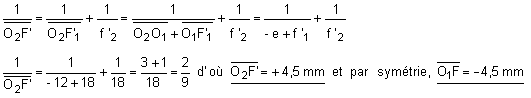

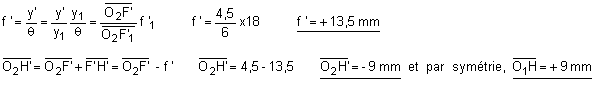
2ème solution (formules de Gullstrand) :
Les formules de Gullstrand permettent de calculer la distance focale image et la position des points principaux du doublet.
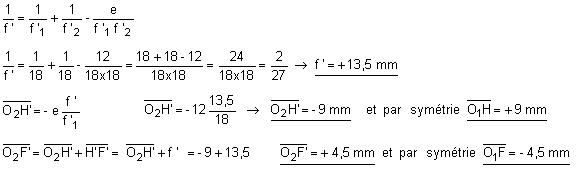
3ème solution (points nodaux et antinodaux) :
Cette solution originale, spécifique aux doublets symétriques, est associée à deux tracés de rayons remarquables :
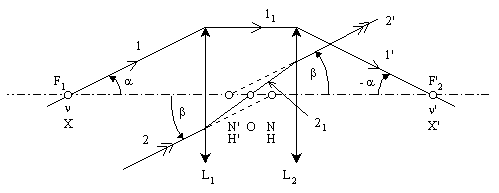
- Un rayon intermédiaire parallèle à l'axe optique (11) a pour conjugué image à travers L2 le rayon (1') qui passe par F'2, et pour conjugué objet à travers L1, le rayon (1) qui passe par F1 ; du fait de la symétrie, les angles a
et a
' sont opposés, et les points F1 et F'2 sont les points antinodaux du doublet (n
et n
' ) ; comme les milieux extrêmes du doublet sont identiques, ces points sont confondus avec les points antiprincipaux du doublet X et X'.
- Un rayon intermédiaire (21) qui passe par le milieu O du doublet, a pour conjugué image à travers L2 et pour conjugué objet à travers L1 les points nodaux du doublet N et N' ; en effet, pour des raisons de symétrie, les rayons (2) et (2') forment avec l'axe optique des angles égaux (b
= b
'). Les milieux extrêmes étant identiques, ces points nodaux sont confondus avec les points principaux du doublet H et H'.
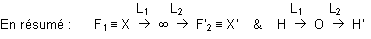
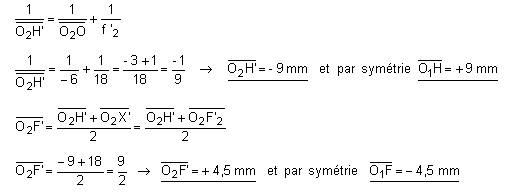
2) 1ère solution (méthode des foyers) :
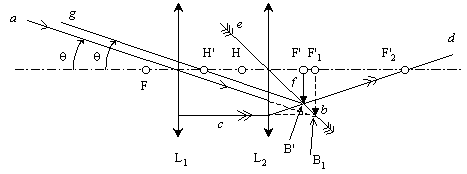
- On trace un rayon objet incliné de q
par rapport à l'axe optique, et passant par le centre optique de L1.
Ce rayon n'est pas dévié.
- Son intersection avec le plan focal image de L1 donne y1 image de l'objet à l'infini de diamètre apparent q
à
travers L1.
- Le bord inférieur de y1, B1, est défini par le rayon intermédiaire parallèle à l'axe optique,
- qui se réfracte à travers L2 en passant par F'2,
- et par le rayon intermédiaire qui passe par le centre optique de L2 et n'est pas dévié.
- L'intersection des deux rayons réfractés donne le bord inférieur de y', B', image de y1 à travers L2.
Cette image est dans le plan focal image [F'] du doublet.
- La parallèle au rayon a menée de B' coupe l'axe optique en H', point principal image du doublet.
F et H sont enfin construits par symétrie par rapport au milieu du doublet.
2 ème solution (système centré) :
C'est la méthode la plus classique. Elle repose sur les définitions des points cardinaux (foyers et points principaux) dans un système centré.
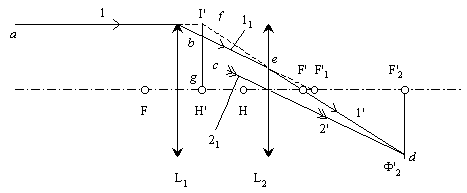
- Le rayon objet ( 1 ) parallèle à l'axe optique est réfracté par L1
- suivant un rayon (11) qui passe virtuellement par F'1.
- Un rayon annexe intermédiaire ( 21 ) , passant par le centre optique de L2, et parallèle à b n'est pas dévié ;
- il coupe le plan focal image de L2 en un foyer secondaire image F
'2,
- par lequel passe ( 1' ), le réfracté de (11) par rapport à L2 ; ce dernier coupe l'axe optique en F', foyer principal image du doublet.
- L'intersection I' des rayons ( 1 ) et ( 1' ) appartient au plan principal image du doublet [H'].
- Le point principal H' image est obtenu en abaissant de I' la perpendiculaire à l'axe optique.
F et H sont enfin construits par symétrie par rapport au milieu du doublet.
3ème solution (points nodaux et antinodaux) :
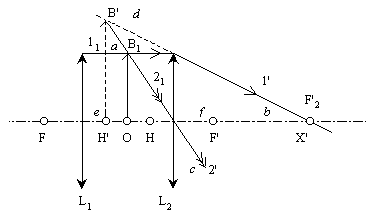
- L'image intermédiaire OB1 est placée sur l'axe optique, à mi-distance de L1 et L2.
Le point B1 est défini par le rayon (11), parallèle à l'axe optique,
- qui se réfracte vers F'2, confondu avec le point antiprincipal image du doublet,
- et le rayon ( 21 ), qui passe par le centre optique de L2 et n'est pas dévié, après réfraction par cette lentille
- L'image B' de B1 à travers L2 est à l'intersection des rayons ( 1' ) et ( 2' ).
- Le pied de la perpendiculaire menée de B1 à l'axe optique est le point principal image H' du doublet.
- Le foyer principal image F' est à mi-distance de H' et X'.
|