6. Lunette de Kepler
1) Une lunette de Kepler comprend un objectif L1 et un oculaire L2.
f '1 = + 250 mm ; f '2 = + 50 mm.
La lunette est afocale.
1) Déterminer la distance qui sépare les deux lentilles.
2) Rappeler la définition du grossissement, puis le calculer.
3) Calculer les champs de la lunette sachant que l'objectif est ouvert à f/10 et l'oculaire à f/5.
4) Comment faudrait-il procéder pour éliminer le champ de contour ?
5) Le plan principal objet de l'œil de l'observateur emmétrope est confondu avec le plan focal image de l'oculaire. A quelle distance de l'objectif se trouve l'objet pour une accommodation de l'observateur de 5 dioptries ?
La lunette n'est plus afocale.
Elle est mise au point à l'infini par un myope de réfraction axiale principale égale à 3 dioptries et qui n'accommode pas.
6) Comment l'oculaire a-t-il été réglé ?
7) Quels sont les champs de la lunette, le champ de contour ayant été éliminé par le procédé défini au 4) ?
1) Comme la lunette est afocale, l'image qu'elle donne d'un objet à l'infini est rejetée à l'infini.
L'image intermédiaire appartient au plan focal image de la première lentille qui est confondu avec le plan focal objet de la seconde lentille : [F'1] º [F2].
La confusion des deux foyers intermédiaires s'écrit :
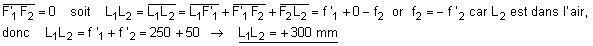
2) La chaîne des conjugaisons sur l'axe et celle des images s'écrivent :
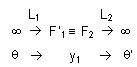
où q et q' représentent les diamètres apparents de l'objet et de l'image, et y1, la taille de l'image intermédiaire.
Le grossissement du système afocal est le rapport du diamètre apparent de l'image au diamètre apparent de l'objet.
Une décomposition de ce rapport image/objet, faisant intervenir l'image intermédiaire, permet de faire apparaître les caractéristiques image/objet de l'objectif et de l'oculaire :
En valeur absolue,
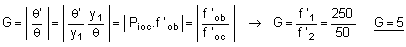
L'oculaire est utilisé de façon intrinsèque, car il donne une image à l'infini et le diamètre apparent de cette image est ainsi indépendant de la position de l'observateur.
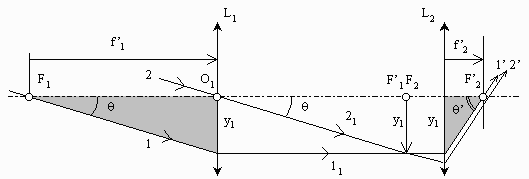
L'expression du grossissement aurait pu être obtenue à partir de la construction graphique ci-dessus :
- Le bord supérieur de l'objet est défini par deux rayons parallèles remarquables, l'un passant par le foyer principal objet de l'objectif (1), l'autre par le centre optique (2). Ces deux rayons réfractés suivant (11) et (21) se focalisent dans l'espace intermédiaire en B1. (11) parallèle à l'axe optique est ensuite réfracté vers le foyer principal image de l'oculaire (1'). (2') est parallèle à (1').
- Les deux triangles grisés ont un côté égal à y1 et des angles sur l'axe optique respectivement égaux à q et q'. Le rapport des tangentes de ces angles donne le grossisement de la lunette afocale.
Remarque :
Le grossissement algébrique, défini avec des angles q et q' orientés à partir de l'axe optique, serait négatif : Ga = - 5, le signe moins traduisant le fait que l'on voit « à l'envers » à travers une lunette de Kepler.
3) Les diamètres d'ouverture de l'objectif et de l'oculaire sont :
250 / 10 = 25 mm et 50 / 5 = 10 mm.
1ère solution (étude des champs dans l'espace intermédiaire) :
Un point objet à l'infini dans la direction de l'axe optique a pour image F'1, confondu avec F2.
Les deux diaphragmes définis par l'ouverture des lentilles L1 et L2 appartiennent à l'espace intermédiaire. Les rayons d'ouverture sont vus à partir de F'1 sous des angles a1 et a2, tels que :
tana1 = 12,5 / 250 = 1 / 20 et tana2 = 5 / 50 = 1 /10.
C'est l'angle qui a la plus petite tangente qui est le plus petit, à savoir a1.
L1 est donc la pupille intermédiaire de la lunette.
L1 est également diaphragme d'ouverture, c'est à dire le diaphragme matériel qui correspond à la pupille, et aussi pupille d'entrée de la lunette, car le plan de L1 est un plan double (il est confondu avec les plans principaux de la lentille).
Comme le système ne comprend que deux diaphragmes, L2 est nécessairement lucarne intermédiaire. Le diaphragme matériel qui lui correspond : L2 lui-même, est diaphragme de champ de la lunette et aussi lucarne de sortie.
Dans l'espace intermédiaire, le faisceau utile de sommet F'1 s'appuie sur la pupille intermédiaire L1.
Pour un point image intermédiaire en dehors de l'axe, le faisceau utile conserve approximativement son ouverture angulaire jusqu'à la position PL1, qui correspond à la limite du champ de pleine lumière intermédiaire.
Au delà, le faisceau est entamé par la lucarne intermédiaire, et son ouverture angulaire diminue continuement.
La limite du champ moyen théorique intermédiaire M1 est obtenue quand le faisceau utile n'est plus défini que par la moitié de la pupille intermédiaire.
La limite du champ total intermédiaire T1 est enfin obtenue lorsque le faisceau utile ne se réduit plus qu'à un seul rayon qui tangente les bords de la pupille intermédiaire et de la lucarne intermédiaire situés d'un même côté de l'axe optique.
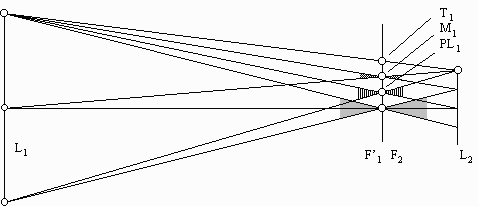
Les trois rayons qui définissent dans le plan de l'image intermédiaire les trois champs intermédiaires s'appuient sur le bord supérieur de la lucarne et sur le bord inférieur, le centre et le bord supérieur de la pupille.
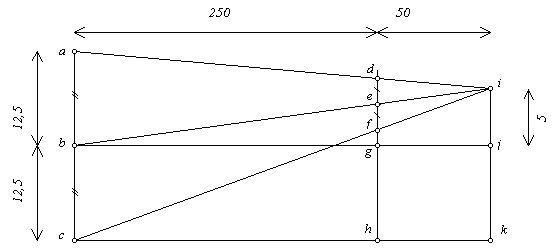
b, centre de la pupille intermédiaire est le milieu de ac ; d'après le théorème de Thalès, e sera de même le milieu de df. En conséquence, le rayon du champ total intermédiaire est :
RT1 = gd = 2ge - gf = 2RM1 - RPL1
Calcul du champ moyen intermédiaire :
Les triangles bge et bih sont semblables (angles égaux deux à deux), d'où
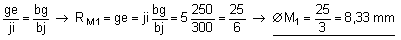
Calcul du champ de pleine lumière intermédiaire :
Les triangles chf et cki sont semblables (angles égaux deux à deux), d'où
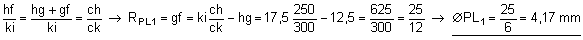
Calcul du champ total intermédiaire :
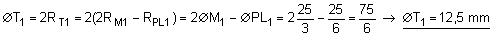
Calcul des champs-objet et des champs-image :
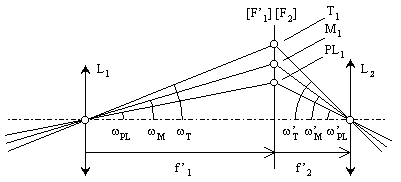
Les champs angulaires objet et image se déduisent simplement des champs intermédiaires (cf. sché-ma ci-dessous).
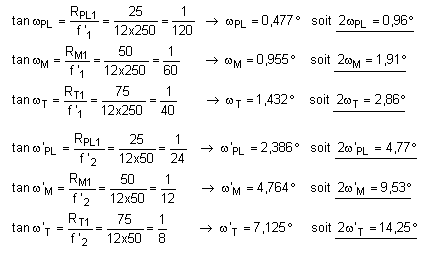
Remarque :
Les champs satisfont les mêmes relations image/objet que les conjugués successifs à travers les lentilles d'un objet étendu (à savoir, distance focale de L1 pour la première conjugaison et puissance intrinsèque de L2 pour la seconde conjugaison).
2ème solution (étude des champs dans l'espace objet) :
Le point objet sur l'axe étant rejeté à l'infini, le faisceau utile qui lui est associé est un faisceau paral-lèle à l'axe optique et qui s'appuie sur la pupille d'entrée de la lunette. Cette pupille d'entrée est le plus petit des diaphragmes ramenés, par conjugaison, dans l'espace objet.
L1 appartient à l'espace objet.
Le conjugué objet de L2 à travers L1 est noté L21. Il est obtenu en position et grandeur par les formules de Descartes :
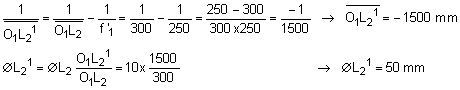
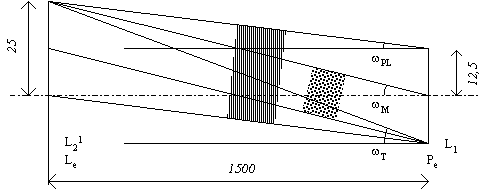
L1 qui est le plus petit des diaphragmes-objet est la pupille d'entrée de la lunette. L21 est donc la lucarne d'entrée.
Les faisceaux utiles issus d'un point à l'infini sur l'axe, d'un point à la limite du champ de pleine lumière objet et d'un point à la limite du champ moyen objet sont représentés sur le schéma ci-dessus, de même le rayon à la limite du champ total objet.
Les demi-angles de champ wPL, wM et wT se calculent aisément à partir des rayons d'ouverture de la lucarne et de la pupille d'entrée, et de la distance qui les sépare :
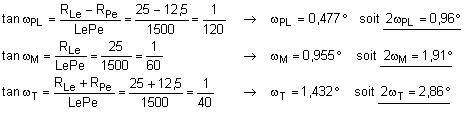
Les champs-image sont obtenus à partir du grossissement de la lunette :

4) Pour éliminer le champ de contour, c'est-à-dire la couronne comprise entre le champ de pleine lumière et le champ total où la luminance diminue continuement du fait de la réduction de l'ouverture du faisceau utile, il faut placer un diaphragme dans le plan d'une image réelle, ici en [F'1], et lui donner le diamètre du champ de pleine lumière en ce point, à savoir 4,17 mm.
5) Un point objet A sur l'axe a pour images successives, à travers L1 et L2, A1 et A'.
En appliquant aux deux conjugaisons la formule de Newton, on obtient :
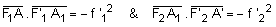
puis en divisant la première équation par la seconde et en tenant compte du fait que les points F'1 et F2 sont confondus, on obtient :
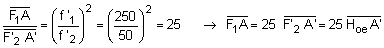

6) Pour effectuer la mise au point à l'infini sans accommoder, le myope doit déplacer axialementt l'oculaire de façon à placer l'image instrumentale A' dans son plan remotal.
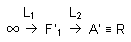
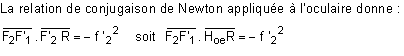
En appelant t le déplacement axial de l'oculaire (cf schéma ci-dessous) et R la réfraction axiale principale de l'observateur,
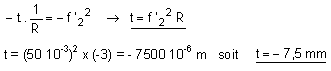
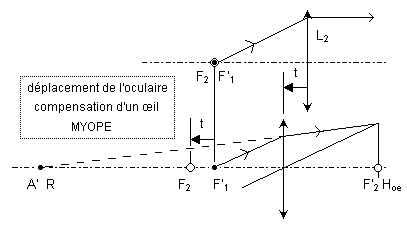
L'oculaire a été déplacé dans le sens inverse de celui de la lumière (cas du myope).
Dans le cas de l'hypermétrope, il aurait été déplacé dans le sens de la lumière.
7) Le diaphragme qui élimine le champ de contour a été placé dans le plan focal image de l'objectif. Le champ objet - qui se réduit au champ de pleine lumière - est inchangé :
2wPL = 0,96°
Comme le champ intermédiaire est inchangé, le champ image, défini dans le plan du Remotum, est calculé à partir du grandissement de l'oculaire :
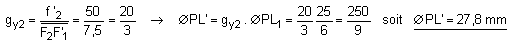
|