1. Principe de Fermat et équation du 4^e degré

2. Principe de Fermat et dioptre sphérique

J.Hormière, le 15 novembre 2000

1	Introduction L'optique géométrique classique est souvent introduite à partir du principe de Fermat, d'où l'on déduit la propagation rectiligne dans les milieux homogènes, le retour inverse et les lois de réflexion et réfraction. La loi de Descartes-Snell, ou loi des sinus, permet de calculer et de construire un rayon réfracté par un dioptre, à partir du rayon incident et des indices de réfraction des deux milieux. Mais une question n'est généralement pas abordée : Comment calculer ou construire le trajet effectivement suivi par la lumière pour relier deux points A et B, le premier situé dans le premier milieu, et le second dans le second ? Question qui se réduit à une autre, à savoir : Déterminer le point d'incidence I sur le dioptre, tel que AI et IB correspondent au trajet suivi par la lumière pour relier les deux points. Les divers livres que j'ai pu consulter n'abordent pas cette question.
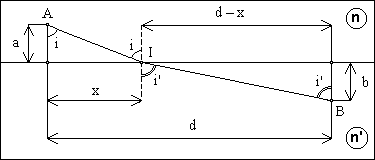
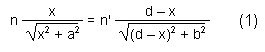
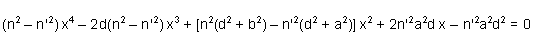
2	Exemple du dioptre plan En annulant la dérivée du chemin optique (AB) = n (AI) + n' (IB) on obtient la loi des sinus : n.sini = n'.sini', dont l'expression analytique est donnée par la relation (1) ci-dessous. En élevant au carré et après développement, on obtient l'équation du quatrième degré : Cette équation peut être mise sous la forme :
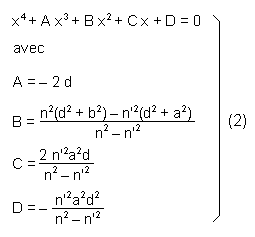
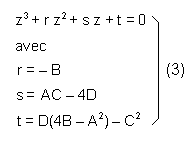
3	Théorie générale Méthode développée par A.Angot dans ses « Compléments de Mathématiques » Éditions de la REVUE D'OPTIQUE (1961) p.696-698. Pour résoudre l'équation du 4e degré, on passe par l'équation du 3e degré suivante : Soit Z sa plus grande racine réelle. Pour l'obtenir il faut résoudre l'équation du 3e degré (3). On fait un changement de variable : z = u - r / 3 et l'équation devient :
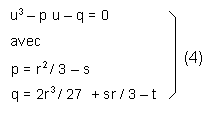
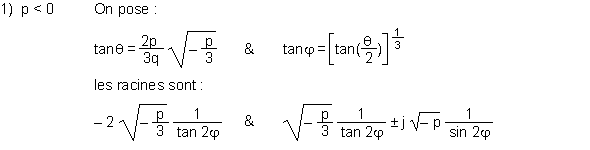
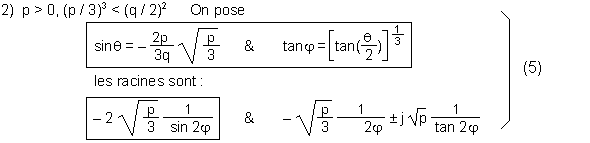
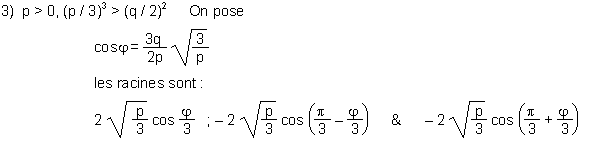
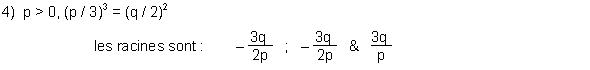
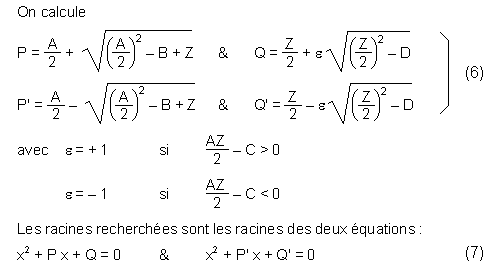
4	Exemple de calcul On peut remarquer, à partir des valeurs de A, B, C et D, que l'on aura toujours : s = 0 p = r2 / 3 > 0 (p / 3)3 - (q / 2)2 < 0 (ce dernier résultat n'est pas démontré, il est simplement vérifié par le calcul sur de multiples exemples) La solution réelle de l'équation du troisième degré réduite sera donc toujours la même (voir encadré plus haut). 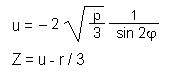On fera toutefois attention au calcul de Z, du fait du changement de variable : Supposons : n = 1 ; n' = 1,5 ; a = 200 mm ; b = 100 mm ; d = 40 mm Les calculs effectués sur le tableur Excel donnent les résultats suivants : A (mm1) B (mm2) C (mm3) D (mm4) - 8,000E+01 + 6,560E+04 - 5,760E+06 + 1,152E+08 r (mm2) s (mm4) t (mm6) - 6,560E+04 0 - 3,6864E+12 p (mm4) q (mm6) k* (mm12) + 1,434E+09 + 2,460E+13 - 4,194E+25 sinq q (rad) tanj j (rad) - 8,501E-01 - 1,016E+00 - 8,227E-01 - 6,884E-01 Z (mm2) e + 6,644E+04 + 1 P (mm1) Q (mm2) P' (mm1) Q' (mm2) + 9,348E+00 + 6,465E+04 - 8,935E+01 + 1,782E+03 d (mm2) d ' (mm2) - 2,585E+05 + 8,558E+02 x1 x2 x'1 (mm) x'2 (mm) imaginaire imaginaire + 5,930E+01 + 3,005E+01 * k = (p / 3)3 - (q / 2)2 On retiendra uniquement la solution x'2, car le point I recherché correspond à x compris entre 0 et d, c'est-à-dire entre 0 et 40 mm. La solution est x = 30,05 mm. On vérifie ce résultat : sini = 30,05 / racine(30.052 + 2002) = 0,149 sini' = 9,95 / racine(9.952 + 1002) = 0,099 1.5 sini' = 1,5 x 0,099 = 0,149     C.Q.F.V. Les racines peuvent être obtenues par tracé de la courbe : on trouve x = 30 mm et x = 60 mm (voir figure ci-dessous).
5	Conclusions Le principe de Fermat appliqué au dioptre plan conduit à une équation du quatrième degré, qui se résout, pourrait-on dire, de façon classique. De plus le calcul se trouve quelque peu simplifié, et c'est toujours le même type de solution que l'on rencontre. Certains points pourraient cependant être approfondis : le signe de (p / 3)3 - (q / 2)2 toujours négatif ; l'interprétation de la seconde racine en dehors du domaine (0 ; d) ; l'application au dioptre sphérique ; etc. Enfin si les traités d'Optique Géométrique n'abordent pas cette question de la recherche du point d'incidence I, c'est peut être parce que la question n'est pas pertinente ou bien alors, que les physiciens ne prisent guère les équations du troisième et du quatrième degré. Il est vrai, à leur décharge, que d'autres méthodes existent, comme par exemple la méthode des dichotomies successives, qui permettent d'obtenir très rapidement une solution précise. J'oubliais... La réponse à la question posée au début n'est pas complète. Il manque la solution graphique : géomètres, à vos règles et compas ! Pour les amateurs, un fichier Excel contenant des programmes en VBA pour le calcul exact, la méthode des dichotomies et la méthode de Newton à ...

Suite...


Retour au Menu