Principe de Fermat et dioptre sphérique

J.Hormière, le 1^er mars 2001

1	Introduction L'application du principe de Fermat au dioptre sphérique conduit à la résolution d'une équation du 6e degré. Il n'est pas question d'aborder ici cette résolution : on a vu précédemment l'équation du 4e degré, et c'est bien suffisant ! On va donc reprendre la méthode des dichotomies successives, extrêmement efficace dans ce type de problème.
2	Exemple du dioptre sphérique On étudie le cas d'un dioptre convexe par rapport à la lumière incidente. Le cas du dioptre concave se déduit en inversant simplement le sens de la lumière. Soit un point A, dans le premier milieu d'indice n, et un point B, dans le second milieu d'indice n'. Le point d'incidence du rayon qui relie A et B se trouve sur le plus petit des deux arcs de cercle : 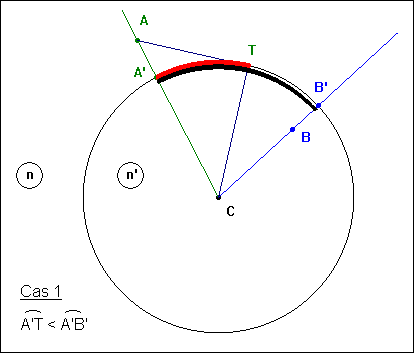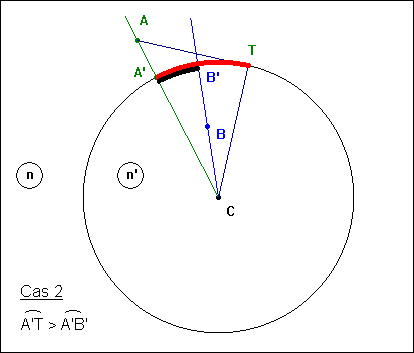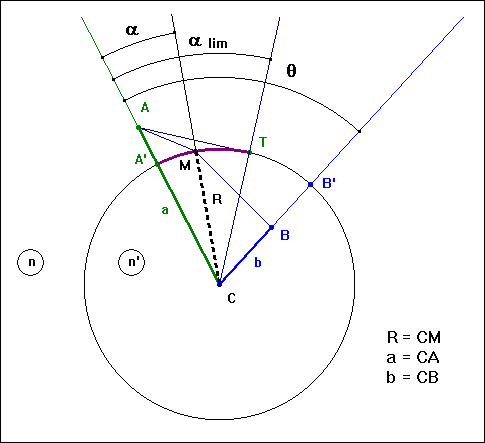A'B' (A' et B' sont les intersections des demi-droites CA et CB avec le dioptre) A'T (AT est la tangente au dioptre du côté de B') Soit un point M de l'arc utile, paramétré par l'angle a. Le chemin optique entre A et B est : L = n.AM + n'.MB Le théorème de Pythagore généralisé appliqué aux triangles CAM et CBM donne : AM2 = a2 + R2 - 2 a.R.cosa MB2 = b2 + R2 - 2 b.R.cos(q - a) on en déduit l'expression du chemin optique, et sa dérivée : 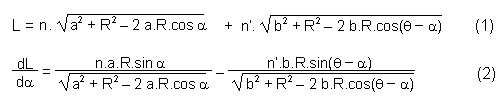Le point d'incidence I correspond à un extremum du chemin optique et donc à une valeur de l'angle a qui annule la dérivée du chemin optique. L'équation dL / da = 0 conduit, après élévation au carré pour éliminer les racines carrées, puis choix de l'inconnue x = sina, à une équation du 6e degré. La méthode de dichotomies successives utilisée pour trouver une valeur approchée de la racine recherchée est développée ci-après.
3	Méthode des dichotomies successives Le programme en Visual Basic ci-dessous permet de suivre la méthode de calcul : Procédure Sub en VBA pour Excel* 95-97-2000 * marque déposée de Microsoft Corporation voir au bas de la page le fichier téléchargeable " fermatds.zip " Sub dicho() nom de la procédure Pi = 3.14159 Dim a1, a2, an, eps As Double calculs en double précision Dim a, b, g, h, n, p, r, t As Double n = Range("C8") cellule : de l'indice n p = Range("D8") - de l'indice n' r = Range("E8") - du rayon de courbure R a = Range("F8") - de la distance a b = Range("G8") - de la distance b g = Range("H8") - de l'angle q h = Range("I13") - de l'angle alim If h > g Then détermination de l'arc utile t = g cas q < alim Else t = h cas q > alim End If eps = t / 10000 précision sur a a1 = 0 a2 = t Do While (a2 - a1) > eps procédure de boucle de calcul : tant que l'intervalle sur lequel on calcule le produit f(a1).f(an) (où a1 et an sont les limites de l'intervalle) reste supérieur à eps, on répète la procédure an = (a1 + a2) / 2 division par deux de l'intervalle de calcul If (n * a * r * Sin(Pi * a1 / 180) / Sqr(a ^ 2 + r ^ 2 - 2 * a * r * Cos(Pi * a1 / 180)) - p * b * r * Sin(Pi * (g - a1) / 180) / Sqr(b ^ 2 + r ^ 2 - 2 * b * r * Cos(Pi * (g - a1) / 180))) * (n * a * r * Sin(Pi * an / 180) / Sqr(a ^ 2 + r ^ 2 - 2 * a * r * Cos(Pi * an / 180)) - p * b * r * Sin(Pi * (g - an) / 180) / Sqr(b ^ 2 + r ^ 2 - 2 * b * r * Cos(Pi * (g - an) / 180))) < 0 Then Si f(a1).f(an) < 0 Alors a2 = an Else Sinon a1 = an End If Loop Range("J13") = an affichage du résultat dans la cellule J13 End Sub
4	Exemple de calcul Considérons l'exemple suivant: n = 1 n' = 1,5 R = 100 mm a = 130 mm b = 80 mm q = 40° alim = Arccos(R / a)= Arccos(100 / 130) = 39,72° Le calcul donne : a = 26,57° Remarque : Si l'on choisit q = 60°, on obtient a = 39,71° qui correspond, aux arrondis près, à alim. Cela vient du fait que le point B ne peut être atteint par un rayon issu de A, car il appartient à la zone d'ombre définie par le bord de la nappe tangentielle de la caustique d'aberration sphérique du dioptre et le bord du faisceau marginal. 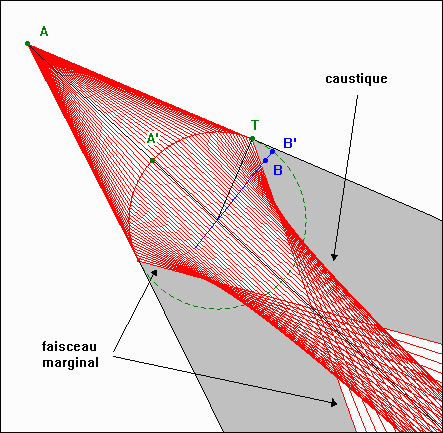Les deux schémas suivants représentent la solution sur le logiciel Cabri II géomètre dans les deux cas de figure. Une valeur approximative de la différentielle du chemin optique est calculée par dL = n(A'M - A'M*) + n'(MB - M*B). M* est un point du dioptre, tel que angle(MCM*) = d(alpha) = 0,1° k.dL est reporté sur le rayon CM : k.dL = Mm (k = 300) Le lieu de m est une courbe qui coupe l'arc SA'T quand il existe une solution (B dans le faisceau réfracté), et ne le coupe pas quand il n'y a pas de solution (B dans l'ombre du faisceau réfracté).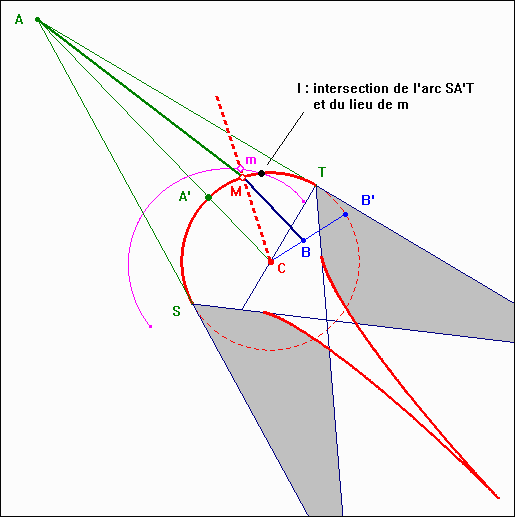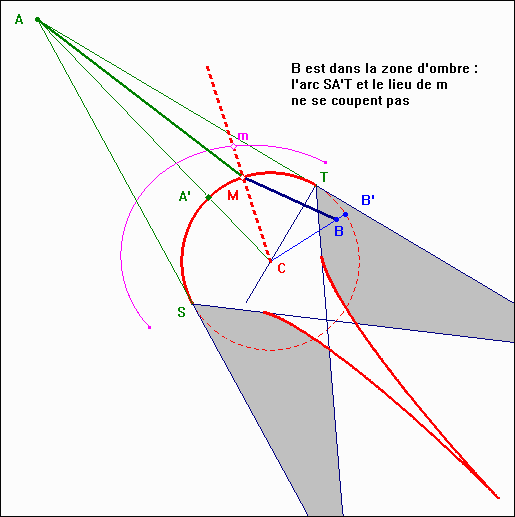
5	Conclusions Deux points A et B appartenant aux deux milieux d'un dioptre sphérique ne sont pas nécessairement reliés par un rayon lumineux. En effet le problème de Fermat qui consiste à rechercher un extremum du chemin optique n.AM + n'.MB, où M est un point du dioptre, n'admet pas toujours de solution. Quand cette solution existe, la méthode des dichotomies successives est particulièrement appropriée pour déterminer le point d'incidence I. C'est la structure du faisceau issu de A, réfracté par le dioptre, avec sa caustique d'aberration sphérique qui définit le volume des points B accessibles. Pour les amateurs d'Excel et de Cabri II géomètre, deux fichiers devraient apporter plus de lumière...

Première partie


Retour au Menu