1. Le texte du Sidereus Nuncius

Galileo Galilei, Le Messager des Étoiles traduction de Fernand Hallyn Éditions du Seuil 1992 / p. 118 et 119 Pour faciliter la lecture du texte de Galilée, je l'ai découpé en éléments, suivis chacun de petits commentaires.
« Primo enim necessarium est, ut sibi Perspicillum parent exactissimum, quod obiecta perlucida, distincta et nulla caligine obducta repræsentet;	« D'abord, en effet, il est nécessaire qu'ils se fabriquent une Lunette de très grande précision, qui puisse représenter les objets brillants, distincts, et sans aucun obscurcissement ;
1. Galilée insiste dès le début sur la qualité de la lunette. Il ne s'agit pas de camelote ! Brillants et sans aucun obscurcissement renvoient à la bonne transparence des verres et à leur bonne homogénéité, et distincts, au bon surfaçage (qualité du poli et de la courbure), à des aberrations géométriques et chromatiques réduites (dues à la faible ouverture de l'objectif), ainsi qu'au grossissement élevé (une lunette de grossissement 2 ou 3 ne permet pas d'observer les satellites de Jupiter) qui fait voir les choses plus précisément, comme si elles étaient plus proches. cf. l'Optique d'Euclide (traduction de Paul Van Eecke, Blanchard 1959, page 2) : « Proposition II (Théorème). Parmi les grandeurs situées à distance, celles qui sont situées plus près, sont vues d'une manière plus distincte. »
eademque ad minus secundum quatercentuplam rationem multiplicet; tunc enim illa bisdecuplo viciniora commonstrabit:	il faut que cette même Lunette agrandisse au moins quatre cents fois, car alors elle montrera les objets vingt fois plus proches ;
2. Le grossissement est aujourd'hui uniquement représenté par un rapport d'angle (notion unidimensionnelle). Galilée le considère ici comme un rapport d'aires (notion bidimensionnelle). Cela présente un intérêt réel lorsque l'on s'intéresse au nombre de détails discernables sur l'image de l'objet. Ainsi la lunette de grossissement (au sens du rapport des angles) égal à 20, permet de discerner schématiquement 20 fois plus de détails dans une direction donnée, mais 400 fois plus de détail sur une surface donnée - comme la surface de la lune par exemple. L'explication du grossissement par un gain de proximité est aujourd'hui encore utilisé dans les argumentaires de vente pour les jumelles et les lunettes terrestres. Elle est dans la pure lignée de l'optique euclidienne : cf. la Proposition V de l'Optique d'Euclide : « Des grandeurs égales inégalement distantes apparaissent inégales, et celle qui est située plus près de l'œil apparaît toujours plus grande »
nisi enim tale fuerit Instrumentum, ea omnia quæ a nobis conspecta sunt in cælis, quæve infra enumerabuntur, intueri tentabitur frustra.	en effet, si l'Instrument n'est pas tel, on tentera en vain de porter le regard sur tous ces phénomènes que nous avons aperçus dans les cieux et qui seront énumérés plus loin.
3. Allusion aux descriptions qui vont suivre : surface de la lune, constellations, satellites de Jupiter.
Ut autem de multiplicatione instrumenti quilibet parvo negotio certior reddatur, circulos binos aut quadrata bina chartacea contornabit, quorum alterum quatercenties altero maius existat; id autem erit tunc, cum maioris diameter ad diametrum alterius longitudine fuerit vigecupla:	Et pour s'assurer sans grande peine du pouvoir d'agrandissement de l'Instrument, on tracera deux cercles ou deux carrés de papier dont l'un soit quatre cents fois plus grand que l'autre, ce qui sera le cas lorsque le diamètre du plus grand aura vingt fois la longueur du diamètre de l'autre.
4. Le terme à nouveau utilisé pour qualifier le grossissement multiplicatione, après multiplicet, fait directement référence aux mathématiques : c'est un facteur multiplicateur, un facteur applicable aux aires dans son sens premier, aux longueurs ou aux angles dans son sens second. L'opérateur euclidien, auquel Philippe Hamou fait référence dans l'extrait cité plus loin, pourrait alors se traduire par multiplicateur (ou diviseur) euclidien, car la géométrie traite, entre autres, du rapport des grandeurs de même nature, se mêlant ainsi à une théorie des proportions que Galilée utilisait dès la fin du XVe siècle dans son étude de la chute des corps. Comment mesurer le grossissement de la lunette ? La méthode que Galilée décrit parfaitement est toujours utilisée.
deinde superficies ambas in eodem pariete infixas simul a longe spectabit, minorem quidem altero oculo ad Perspicillum admoto, maiorem vero altero oculo libero;	Ensuite, on regardera simultanément de loin les deux surfaces fixées au même mur, en observant le plus petit d'un œil appliqué à la Lunette et le plus grand de l'autre œil resté libre
5. L'observation simultanée est importante, sinon, c'est de mémoire que l'on doit comparer les diamètres apparents. L'expérience conduit, pour des grossissements pas trop élevés, à une valeur imaginée plus petite que la valeur nominale (mesure par défaut).
commode enim id fieri licet uno eodemque tempore, oculis ambobus adapertis:	(cela peut se faire facilement, en même temps, les deux yeux ouverts) :
6. Cette remarque montre que Galilée était un bon praticien. Les débutants en effet ont toujours de la peine à garder les deux yeux ouverts et les utiliser vraiment tous deux, car comme les deux images rétiniennes sont différentes (vision à l'œil nu et vision à travers l'instrument), la tendance est soit de neutraliser l'image vue à l'œil nu, soit de fermer carrément cet œil qui ne regarde pas à travers l'instrument. Ces deux yeux ouverts sont également une condition de bon réglage de l'oculaire lorsqu'on effectue la mise au point ; si l'œil nu regarde au remotum, alors l'oculaire sera réglé de façon à renvoyer l'image instrumentale au remotum, ce qui permettra de longues observations, sans fatigue oculaire, ni maux de tête.
tunc enim figuræ ambæ eiusdem apparebunt magnitudinis, si Organum secundum optatam proportionem obiecta multiplicaverit.	alors, en effet, les deux figures apparaîtront de même grandeur, si l'Instrument agrandit les objets selon la proportion désirée.

7. Galilée suppose en définitive, dans cette procédure, le grossissement G connu a priori ; il ne s'agit donc que d'une vérification. Alors comment ce grossissement avait-il été évalué ? La connaissance des courbures des deux lentilles (plan-convexe et plan-concave) suffit pour déterminer G, car G =  Rconvexe/Rconcave. En effet, la formule des lunetiers (non connue au début du XVIIe siècle ?) donne : 1/f ' = (n - 1)(1/R1 - 1/R2), où R1 et R2 sont les rayons de courbure algébriques des dioptres. Pour une lentille plan-convexe ou plan-concave, l'un des rayons est infini, et son inverse nul ; la focale du verre est f ' =R/(n - 1). Un indice de réfraction du verre égal à 1,5 donne f ' = 2 R. Comme le grossissement est égal au rapport des focales (G = f 'ob/f 'oc), il est aussi égal au rapport des rayons de courbure. On peut imaginer que Galilée connaissait cette relation car, comme la notion de distance focale n'était pas définie à cette époque, les lentilles ne pouvaient être classées que par leur rayon de courbure.
Consimili parato Instrumento, de ratione distantiarum dimetiendarum inquirendum erit: quod tali artificio assequemur.	Munis d'un Instrument de cette sorte, il nous faudra chercher la méthode permettant de mesurer les distances, ce que nous obtiendrons par la technique suivante.
8. De quelles distances s'agit-il ? Dans l'observation de la lune, Galilée donne des distances linéaires calculées à partir du grossissement de la lunette et de la connaissance du diamètre apparent de la lune et de la distance terre-lune. Pour les satellites de Jupiter il donne les distances angulaires qui les séparent, distances « mesurées selon la méthode exposée plus haut » (FH page 145). La méthode en question est explicitée ci-après.
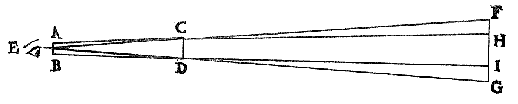
Sit enim, facilioris intelligentiæ gratia, tubus ABCD.	Soit, pour une meilleure compréhension, le tube ABCD.
9. Les premières lunettes sont souvent appelées des tubes. Cette dénomination met l'accent sur ce qui pourrait sembler annexe au physicien, c'est-à-dire la mécanique qui relie deux lentilles. C'est pourtant le tube qui frappait les imaginations, plus peut être que les lentilles mêmes. Il était comme une extension de l'œil : un œil long pour voir au loin : une longue-vue. Le terme latin plus savant que Galilée utilise est Perspicillum : un instrument pour voir au travers. Ainsi, l'appropriation de cet instrument par les savants s'est-elle donc aussi faite par le langage. Au début, le tube c'était pour épater les badauds, et aussi les princes, curieux de tout : à mettre au rang des miroirs déformants et autres curiosités optiques. C'était également un vieux procédé de découpage d'une partie du ciel, pour l'observer plus tranquillement (voir plus loin 11.). Puis, la technique améliorant la qualité des images, il devint l'instrument des astronomes, le Perspicillum de Galilée. Enfin, quand les images qu'il donnait du ciel finirent par être « certifiées conformes » par la plupart des autorités scientifiques de ce temps (le XVIIe siècle), il prit le nom de télescope.
Oculus inspicientis esto E.	Admettons que l'œil de l'observateur soit en E.
10. Le choix de la position de l'œil est très important dans l'explication de Galilée. Ce choix n'est pas explicité par le texte ci-dessus, mais par le schéma optique puis, plus loin, par le raisonnement géométrique. L'œil n'est pas vraiment collé contre l'oculaire, ce qui pourrait paraître tout à fait irréaliste, mais suffisamment proche pour que le sommet de la pyramide visuelle puisse être confondu avec le centre optique de la lentille.
Radii, dum nulla in tubo adessent Perspicilla, ad obiectum FG secundum lineas rectas ECF, EDG ferrentur;	S'il n'y avait pas de lentilles dans le tube, les rayons seraient conduits vers l'objet FG selon les lignes droites ECF, EDG ;
11. Là on retrouve un astronome de la vieille école. Les tubes, sans verre aucun, étaient depuis fort longtemps utilisés pour observer le ciel. Certains y voyaient mieux, paraît-il, qu'à l'œil nu, et se mettaient même au fond de puits, tubes plus larges sans aucun doute, mais ne permettant que l'observation du zénith. L'efficacité de ces tubes est fort contestée. Ils n'améliorent pas objectivement le contraste, tout au plus permettent-ils de mieux faire abstraction de l'environnement et par exemple, de ne pas être ébloui par la pleine lune quand on fait une observation dans son voisinage. L'autre aspect du tube, plus intéressant lui, c'est qu'il permet des mesures angulaires, le diamètre apparent étant donné en radian - si l'œil bien évidemment se place très près de l'extrémité - par le rapport du diamètre du tube à sa longueur
sed, appositis Perspicillis, ferantur secundum lineas refractas ECH, EDI: coarctantur enim, et qui prius liberi ad FG obiectum dirigebantur, partem tantummodo HI compræhendent.	mais si des lentilles sont en place, les rayons sont conduits selon les lignes réfractées ECH, EDI ; ils sont, en effet, rapprochés l'un de l'autre et, alors que, dans le premier cas, ils se dirigeaient librement vers l'objet FG, ils n'en embrasseront plus que la partie HI.
12. Il s'agit là sans aucun doute de rayons visuels, émis par l'œil vers l'objet. Cette façon de voir était chose courante à l'époque de Galilée. Aujourd'hui encore, dans le langage des opticiens, le mot extériorisation renvoie à cette conception de la lumière. L'extériorisation d'une image rétinienne est ainsi définie : lorsqu'un observateur regarde un objet, l'image optique de cet objet ne se trouve pas nécessairement sur la rétine ; la cause peut en être que le sujet n'accommode pas sur l'objet, ou bien que l'objet se trouve simplement en dehors de son parcours d'accommodation. La projection conique de l'image rétinienne, floue dans ce cas-là, dans le plan de l'objet (le centre de projection étant les points nodaux de l'œil supposés confondus) est l'extériorisation proprement dite. On trouve ainsi dans cette notion mâtinée de principe de retour inverse un vestige des rayons visuels.
Accepta deinde ratione distantiæ EH ad lineam HI, per tabulam sinuum reperietur quantitas anguli in oculo ex obiecto HI constituti, quem minuta quædam tantum continere comperiemus.	Après avoir trouvé ensuite le rapport de la distance EH à la ligne HI, on trouvera grâce à la table des sinus l'ouverture de l'angle formé dans l'œil par l'objet HI, dont nous découvrirons qu'il n'est que de quelques minutes.
13. Cette table des sinus n'est pas du tout nécessaire car les angles sont petits. Pour une lunette de grossissement 14, dont l'objectif a une focale de 1,33 m et une ouverture de 26 mm, le demi-angle sous lequel on voit l'objectif à partir de l'oculaire est a, tel que tana = 13/1235 = 1/95 = 0,010527. Une approximation tana = a (rad) donne a = 0,010527 rad, soit 0,60311°. Le calcul avec la tangente donnerait 0,60309°, et avec le sinus, 0,60312°. On voit que l'utilisation de la fonction sinus ne s'impose absolument pas, car l'erreur relative est de l'ordre de 1/20 000 !
Quod si Specillo CD bracteas, alias maioribus, alias vero minoribus perforatas foraminibus, aptaverimus, modo hanc, modo illam, prout opus fuerit, superimponentes, angulos alios atque alios pluribus paucioribusque minutis subtendentes, pro libito constituemus;	Et si nous adaptons contre la lentille CD des feuillets perforés, les uns de grands trous, les autres de petits trous, appliquant tantôt l'un, tantôt l'autre, en fonction du besoin, nous formerons à volonté des angles variés, étendus sur plus ou moins de minutes,
14. Il s'agit d'angles définis dans l'espace objet. Ainsi, avec la lunette précitée, un angle objet q de 1' donne un angle image q' de 14'. Lors de l'observation, les images des objets célestes et du diaphragme placé contre l'objectif ne sont pas dans un même plan. Si la lunette est afocale et si l'observateur regarde à l'infini, comme le plan conjugué du diaphragme à travers l'objectif et l'oculaire se trouve à 88,2 mm en avant de l'oculaire ; il nécessiterait, pour une vision nette, une accommodation de plus de 11 dioptries - ce qui est l'accommodation maximum pour quelqu'un de très jeune (voir plus loin courbe de Duane). Ce bord de diaphragme est donc vu complètement flou. Les mesures restent-elles tout de même possibles ? Nous en reparlerons dans l'étude des champs.
quorum ope Stellarum intercapedines, per aliquot minuta adinvicem dissitarum, citra unius aut alterius minuti peccatum, commode dimetiri poterimus.	à l'aide desquels nous pourrons facilement mesurer les intervalles des Étoiles distantes de quelques minutes l'une de l'autre, sans erreur dépassant une ou deux minutes.
15. Cette précision de mesure semble fort grossière. En admettant la mesure d'un angle objet de 10' et une erreur absolue de 2', l'erreur relative est égale à 20% !
Hæc tamen sic leviter tetigisse, et quasi primoribus libasse labiis, in præsentiarum sit satis; per aliam enim occasionem absolutam huius Organi theoriam in medium proferemus. »	Qu'il suffise cependant, pour le moment, d'avoir légèrement effleuré ces questions, et d'y avoir goûté comme du bout des lèvres ; car nous publierons à une autre occasion la théorie complète de cet Instrument. »
16. Galilée nous aurait-il fait goûter de l'eau, incolore, inodore et sans saveur ? Peut être nous sommes-nous rafraîchis, mais la mémoire de cette eau ne nous en restera pas longtemps.