2. Une théorie « rustique » du grossissement

J.Hormière / 12 février 2002 Dans sa préface au Messager des Étoiles, Fernand Hallyn [1] considère que l'exposé de Galilée sur sa lunette n'est qu'une prétérition [2] et il écrit : « Tout en déclarant que l'étude de la réfraction relève des mathématiques, Galilée se garde bien d'étudier la question à fond sous cet aspect-là. Sur le dessin qui illustre le fonctionnement du télescope dans le Messager des Étoiles, tout comme dans le commentaire qui l'accompagne, il est frappant de constater que la fonction de l'oculaire n'est guère abordée : Galilée situe une réfraction en l'endroit de l'objectif (en CD), mais ne mentionne aucune modification des rayons au moment du passage de l'oculaire (en AB), comme si la forme du verre employé était indifférente. » Philippe Hamou, dans La Mutation du Visible [3], définit la lunette de Galilée comme une lunette « euclidienne » et précise : « L'optique euclidienne étant la science qui nous apprend à raisonner sur les rapports de grandeur et de distance, il pouvait sembler légitime de faire du télescope un simple opérateur euclidien, et de le traiter comme une boîte noire dont le fonctionnement réel n'a pas besoin d'être élucidé. »... « Il nous semble qu'il existe une analogie frappante entre la manière dont Galilée traite le télescope et celle dont il traite l'œil dans les très rares textes où il évoque le mode de fonctionnement de cet organe. Ce qui l'intéresse exclusivement dans les deux cas c'est l'ouverture de l'angle visuel à la sortie de l'organe... ». Ces remarques sont pertinentes, mais insuffisantes me semble-t-il ; en effet, s'il est vrai que l'oculaire joue un rôle évident dans la formation de l'image instrumentale, en réfractant (déviant) les rayons qui le traversent, le schéma de Galilée n'en est pas pour le moins parfaitement correct d'un point de vue optique, même s'il représente un cas particulier. Les rayons qui passent par le centre optique de l'oculaire ne sont pas déviés, et lorsque l'œil de l'observateur est collé contre cet oculaire, le diamètre apparent de l'image instrumentale, quelle que soit sa position, est bien défini à partir du centre optique de l'oculaire. La forme du verre oculaire n'intervient qu'indirectement, dans la distance objectif-oculaire qui, pour un système afocal, est égale à la somme algébrique de la focale de l'objectif et de celle de l'oculaire ; focale de l'objectif et distance objectif-oculaire sont suffisantes pour fixer le grossissement. Ainsi une théorie du grossissement est inscrite comme en filigrane dans la représentation de la lunette que nous fait Galilée. Connaissait-il lui-même et maîtrisait-il cette théorie ? La suite fournira quelques pistes. Je vais d'abord montrer comment, à partir du simple schéma et de deux hypothèses, on retrouve bien le grossissement de la lunette, puis j'essaierai de préciser divers aspects de cette théorie sous-jacente, éminemment euclidienne, pour reprendre l'expression de Hamou, et que je qualifie de « rustique ». Hypothèses 1. L'œil est supposé placé très près de l'oculaire. 2. La lunette est afocale : elle donne d'un objet à l'infini une image à l'infini ou, autrement dit, le foyer principal image de l'objectif coïncide avec le foyer principal objet de l'oculaire. 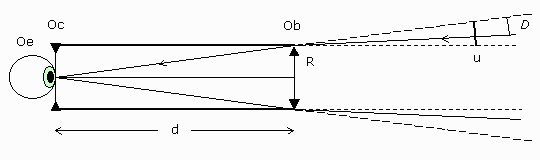Calcul du grossissement L'objet observé à travers le tube de longueur d, sans objectif ni oculaire, est défini par l'angle 2u. Le rayon visuel issu du centre de la pupille de l'œil et passant par le bord supérieur de l'objectif n'est pas dévié par l'oculaire, car il passe par son centre optique. Sur l'objectif la déviation de ce rayon est D. La partie de l'objet observée à travers la lunette et vue sous l'angle 2u correspond à un angle visuel égal à 2(u - D). Le grossissement de la lunette est ainsi égal au rapport des deux angles définis ci-dessus : 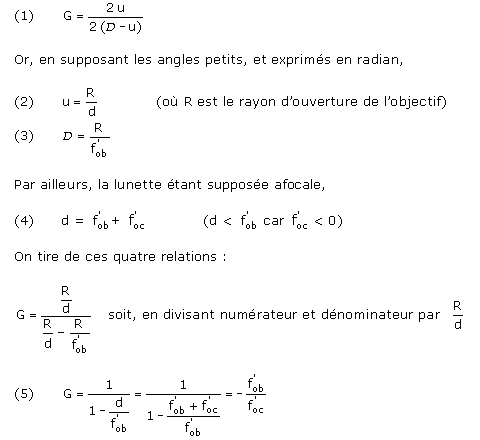ce qui correspond au grossissement classique d'une lunette astronomique ! Mais où sont passées les images ? Dans le schéma de Galilée il n'y a pas de formation d'image à proprement parler (à savoir l'image d'un objet éloigné). Mais on peut toutefois remarquer que le conjugué objet de l'œil à travers l'oculaire et l'objectif apparaît implicitement dans le tracé des rayons. Ce conjugué est virtuel et se trouve derrière l'observateur ; on l'obtient en prolongeant les rayons qui arrivent sur l'objectif. Il permet de comprendre géométriquement le grossissement car, s'il n'y avait pas la lunette, tout se passerait comme si l'œil de l'observateur était plus éloigné de l'objet, et de plus le verrait sous un angle plus petit qu'à travers l'instrument. Dans cette perspective le schéma de Galilée illustre parfaitement la définition du grossissement, c'est-à-dire le rapport du diamètre apparent de l'image au diamètre apparent de l'objet, rapport qui est explicitement confondu avec celui des deux longueurs FG et HI définies dans un plan éloigné choisi arbitrairement [4]. L'objectif fonctionne ainsi comme un transformateur d'ouverture de faisceau, ou plus précisément comme un multiplicateur d'angle visuel. (Un géomètre comme Galilée ne pouvait ignorer que les lentilles convergentes - ou convexes comme l'on disait plutôt, insistant plus sur la forme géométrique que sur l'effet optique - dévient vers l'axe optique les rayons qui les rencontrent en dehors de leur centre. L'effet prismatique observé quand on regarde un objet proche au travers du bord d'une lentille devait aussi être connu de lui.) L'objectif donc augmente l'angle visuel sous lequel l'observateur "embrasse" l'objet, ce qui lui fait mieux en discerner les détails. L'oculaire, par contre, n'est pas vraiment un transformateur d'angle visuel ; il fait simplement voir l'image nette (de façon moderne, on pourrait dire que l'oculaire collé contre l'œil emmétrope le transforme en œil hypermétrope et lui permet ainsi de voir une image qui se trouve derrière lui, dans la partie virtuelle de son parcours d'accommodation), et la vision nette, cela ne peut pas se montrer sur un schéma géométrique, où la réfraction de la lumière dans l'oeil - qui serait en l'occurence une focalisation sur la rétine - n'est pas figurée. Remarques : Il s'agit pour l'oculaire - et je le répète - du cas particulier où le faisceau qui converge au centre optique n'est pas modifié, cas particulier qui coïncide d'ailleurs avec la pratique expérimentale : en effet, pour une lunette à oculaire divergent, le champ perçu est d'autant plus grand que l'œil est proche de l'oculaire. Dans le raisonnement précédent, les angles visuels 2u et 2(u - D) ne représentent pas à proprement parler des champs, et ce d'autant plus que, dans la lunette de Galilée, c'est l'objectif qui est diaphragme d'ouverture (voir chapitre 3). Cela serait uniquement le cas, si la pupille de l'oeil était diaphragmée artificiellement par un sténopé, devenant ainsi diaphragme d'ouverture. Les angles visuels précités correpondraient alors aux champs moyens image et objet du système lunette + oeil. L'Optique prékeplerienne Au début du XVIIe siècle l'explication du grossissement des lunettes repose principalement sur deux observations élémentaires : les lentilles convergentes (tenues assez près de l'œil) grossissent les objets visibles (éloignés), mais en donnent des images floues ; les lentilles divergentes rapetissent ces objets visibles, mais en donnent des images nettes. Dans l'Essayeur (cité par Hallyn, p.44) Galilée reprend ce type d'explication, et pour réaliser ses lunettes, il expérimente, sans pousser plus loin la théorie. J'ai montré précédemment que le grossissement était égal au rapport des rayons de courbure [commentaire 7 du chapitre 1]. La lunette bien conçue relevait donc d'un simple accord entre ces deux rayons et la distance qui sépare les deux lentilles. Mais comment Galilée procédait-il ? On peut imaginer la pratique suivante. La pratique galiléenne L'ordre des verres ne posait pas de problème particulier, puisque Galilée avait déjà utilisé une lunette hollandaise. Le verre convexe (convergent) venait en premier, et le concave (divergent) en second. Pour choisir le grossissement, il fallait trouver les deux courbures adéquates : une grande pour le convexe et une petite pour le concave, avec bien sûr une infinité de solutions. Les limites étaient fixées par les possibilités technologiques dont disposaient les artisans qui travaillaient pour Galilée : outils et qualité de surfaçage, homogénéité et transparence des verres. Les verres choisis, la lunette devait ensuite être ajustée. Le foyer image de l'objectif pouvait toujours être matérialisé sur un écran en y formant, par exemple, l'image d'une fenêtre à contre-jour. La recette, ou le truc, était alors de placer l'oculaire divergent entre le foyer de l'objectif et l'objectif, en usant peut-être de la formule magique : d = 2(R - r) - avec R, rayon de courbure de l'objectif plan-convexe, et r, rayon de courbure de l'oculaire plan-concave. Restait enfin la nécessité de faire varier la distance objectif-oculaire, soit pour assurer la compensation d'une éventuelle amétropie sphérique (myopie ou hypermétropie) de l'observateur, soit pour permettre la mise au point sur un objet rapproché. [1] Fernand Hallyn : Galileo Galilei, Le Messager des étoiles (Éditions du Seuil, 1992), p.42-45. [2] Prétérition : C'est une figure de rhétorique qui consiste à annoncer que l'on ne va pas parler de quelque chose, pour en parler en définitive par ce biais-là. En réalité, la prétérition est ici quelque peu inversée, car Galilée promet pour le lendemain une théorie qu'il ne peut faire la veille... [3] Philippe Hamou : La mutation du visible, Vol. 1 (du Sidereus Nuncius à la Dioptrique cartésienne), Presses Universitaires du Septentrion, 1999, p.102 [4] : C'est le plan où Galilée mesure le grossissement. La navette entre les angles visuels (aujourd'hui devenus diamètres ou angles apparents) et les longueurs de segments disposés transversalement devant l'observateur appartient au langage euclidien. Il suffirait, pour illustrer la confusion du rapport d'angles avec le rapport de longueurs, de retourner les termes de la Proposition V d'Euclide (déjà citée dans le commentaire 2 du premier chapitre) : « Des grandeurs égales inégalement distantes apparaissent inégales, et celle qui est située plus près de l'œil apparaît toujours plus grande » - cf. L'Optique et la Catoptrique (traduction de Paul Van Eecke, Blanchard 1959, page 4) - en « Des grandeurs inégales également distantes apparaissent inégales, et celle qui est la plus grande apparaît toujours plus grande ».