J.Hormière / 13 février 2002
Les lunettes que Galilée utilisa pour l'observation du ciel présentaient deux différences notables
avec les lunettes inventées quelques années auparavant en Hollande. Elles avaient un grossissement
beaucoup plus élevé (les premières lunettes grossissaient de deux à trois fois, alors que celles
de Galilée grossissaient cinq à dix fois plus), et la qualité de transparence et d'homogénéité
des verres utilisés était nettement supérieure.
D'un point de vue optique, une autre différence est à prendre en compte :
c'est l'élément qui dans l'association (lunette + œil) joue le rôle de
diaphragme d'ouverture. En effet, ce diaphragme a une fonction très importante, car il définit la quantité de lumière
qui entre dans l'œil de l'observateur, mais intervient également dans la géométrie des champs.
Rappelons quelques définitions :
- Un système de lentilles sphériques est dit centré lorsque les centres de courbure des différents dioptres qui composent les lentilles sont alignés sur une droite appelée axe optique du système
- Dans un système optique centré, le diaphragme d'ouverture est le diaphragme matériel qui limite l'ouverture d'un faisceau centré.
- Un faisceau est dit centré, dans le cas d'un faisceau cylindrique, si son axe se confond avec l'axe optique du système, et dans le cas d'un faisceau conique, si son sommet est sur l'axe optique.
- Les conjugués du diaphragme d'ouverture dans les différents espaces sont appelés pupilles.
- La pupille d'entrée est le conjugué du diaphragme d'ouverture dans l'espace objet, et la pupille de sortie, le conjugué du diaphragme d'ouverture dans l'espace image de l'instrument.
Nous allons montrer que pour les faibles grossissements, c'est l'iris
de l'œil qui joue ce rôle, alors que pour des grossissements plus élevés,
en l'occurence pour les lunettes de Galilée, c'est l'objectif qui est diaphragme d'ouverture. De là une série
de conséquences que nous évoquerons à la fin de ce chapitre.
Grossissement équipupillaire
Considérons la lunette de Galilée représentée ci-dessous.
- L'objectif est une lentille mince convergente, et l'oculaire, une lentille divergente.
- Ils sont séparés par la distance L.
- Dans l'espace image de la lunette, c'est-à-dire l'espace défini par les rayons situés entre l'oculaire et l'œil, le faisceau issu d'un point objet à l'infini dans la direction de l'axe optique est limité transversalement par la pupille.
- Comme ce faisceau est parallèle à l'axe (lunette afocale), c'est le plus petit des diaphragmes conjugués dans cet espace qui est pupille.
- La pupille d'entrée de l'œil de rayon r (à droite sur le schéma) et l'oculaire, de rayon toujours plus grand, appartiennent à l'espace image de la lunette.
- Le conjugué de l'objectif à travers l'oculaire est limité transversalement par les droites issues du bord de l'objectif et qui passent par le centre optique de l'oculaire.
- Soit x, la distance entre le conjugué image de l'objectif (à travers l'oculaire) et l'oculaire.
- Et considérons le cas limite où ce conjugué a même rayon d'ouverture que la pupille d'entrée de l'œil (cas représenté sur le schéma ci-dessus).
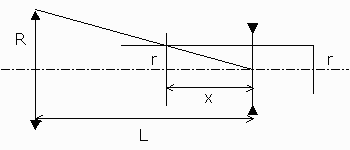
- De la similitude des deux triangles rectangles de côtés respectifs (R, L) et (r, x), on tire la relation (1)
- Comme la lunette est afocale, L est la somme des distances focales images des deux lentilles (2).
- Enfin la relation de conjugaison entre l'objectif et son image à travers l'oculaire donne (3).
- Le grossissement limite, appelé grossissement normal ou grossissement équipupillaire (la pupille de sortie de l'instrument seul a même diamètre que la pupille d'entrée de l'œil) est calculé à partir de ces trois relations.
La condition pour que l'objectif soit diaphragme d'ouverture découle de ces considérations.
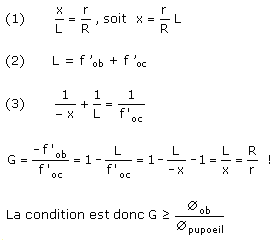
Exemples de grossissements limites :
|
G |
diamètre objectif (mm) |
| 20 |
25 |
30 |
diamètre
pupille œil
(mm) |
3 |
6,67 |
8,33 |
10 |
| 4 |
5 |
6,25 |
7,5 |
| 5 |
4 |
5 |
6 |
Comme en faible lumière la pupille de l'œil se dilate, le grossissement équipupillaire diminue (à ouverture d'objetif constante).
Les lunettes de Galilée
Dans le site italien du Musée d'Histoire de la Science de Florence, on trouve des informations sur deux des lunettes que Galilée aurait utilisées :
« Due cannocchiali appartenuti a Galileo oggi conservati nel Museo di Storia della Scienza. Il primo è costituito da un tubo di legno ricoperto di carta, che contiene un obiettivo biconvesso, distanza focale 1,33 m, apertura utile 26 mm, e un oculare piano concavo. Ha capacità di ingrandimento di 14 volte. Il secondo presenta un tubo di legno ricoperto di pelle rossa, con fregi in oro. l'obiettivo è biconvesso, apertura utile 16 mm, distanza focale 96 cm; non è originale l'oculare biconcavo. Ingrandisce 20 volte. »
http://galileo.imss.firenze.it/multi/luoghi/oggetti/iimsso.html#4
| Lunette 1 |
Lunette 2 |
| f 'ob = 1,33 m ; Øob = 26 mm ; G = 14 |
f 'ob = 0,98 m ; Øob = 16 mm ; G = 21 |
Un diamètre minimum de pupille de 2 mm donne pour ces deux lunettes des grossissements équipupillaires de 26/2 = 13 et 16/2 = 8. Les grossissements des lunettes sont supérieurs à ces valeurs ; l'écart augmente d'ailleurs pour des diamètres de pupille d'œil plus réalistes, c'est-à-dire de l'ordre de 3 à 5 mm.
Une autre façon de raisonner consiste à calculer le diamètre minimum de la pupille de l'œil nécessaire pour que le grossissement dépasse la valeur limite.
Pour la première lunette on trouve 26/14 = 1,8 mm et pour la seconde, 16/21 = 0,8 mm. Ces diamètres, le second en particulier, ne peuvent être atteints qu'en plaçant devant l'œil un sténopé.
| → |
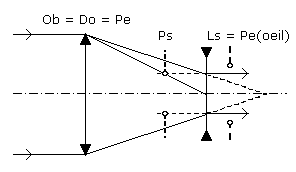
Dans les lunettes utilisées par Galilée, c'est donc l'objectif qui joue le rôle de diaphragme d'ouverture (Do), ainsi que celui de pupille d'entrée (Pe) du système (instrument + œil).
La pupille de sortie (Ps) est le conjugué image de l'objectif à travers l'oculaire.
La pupille d'entrée de l'œil (Pe(œil)) joue le rôle de lucarne de sortie (Ls) de la lunette. |
La première conséquence est, pour un diamètre d'objectif donné et un diamètre de pupille d'œil variable :
- l'invariance de l'éclairement rétinien dans l'observation d'un objet étendu (lune) ;
- l'invariance du flux rétinien dans l'observation d'un objet ponctuel (satellite de Jupiter).
La deuxième conséquence concerne les champs.
Elle va être étudiée dans le chapitre suivant.
|