J.Hormière / février-mars 2002
Les champs des deux lunettes de Galilée citées dans le chapitre précédent peuvent facilement être calculés. C'est ce que nous allons faire afin de mieux préciser les conditions optiques et géométriques d'observation des satellites de Jupiter.
Théorie des champs de la lunette de Galilée
Le diaphragme d'ouverture et ses conjugués appelés pupilles ont été définis précédemment. Complétons ces définitions pour définir les champs en largeur.
On suppose que l'objectif de la lunette est diaphragme d'ouverture. Son conjugué à travers l'oculaire est donc pupille de sortie (Ps) de la lunette.
- Un point objet à l'infini est défini par un faisceau parallèle (ou cylindrique) qui s'appuie sur la pupille d'entrée (Pe) de la lunette, à savoir ici sur l'objectif.
Ce faisceau est réfracté par l'objectif, puis par l'oculaire.
- Le faisceau émergeant de la lentille s'appuie sur la pupille de sortie (Ps).
Cette pupille de sortie est le conjugué de l'objectif à travers l'oculaire.
- Un point objet à l'infini dans une direction oblique inclinée de ω par rapport à l'axe optique est associé à un faisceau parallèle oblique incliné de ω par rapport à ce même axe.
- Lorsque ω croît à partir de zéro degré, le faisceau image réfracté par la lunette reste parallèle (cylindrique) ; son inclinaison croît comme G.ω, où G est le grossissement de la lunette.
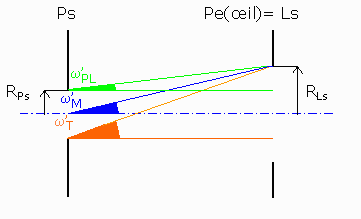
- Pour un angle d'incliaison particulier du faisceau objet ω = ωPL, le diaphragme image qui commence à entamer le faisceau image est la pupille d'entrée de l'œil ; celle-ci joue donc le rôle de lucarne de sortie (Ls) pour la lunette.
- L'iris qui est le diaphragme matériel correspondant à cette lucarne est le diaphragme de champ (Dc) du système (lunette + œil).
- 2 ωPL est le champ objet de pleine lumière (ou de plein éclat).
- Quand l'angle d'inclinaison objet est égal à ωM, le faisceau image qui arrive sur la lucarne de sortie est à moitié diaphragmé ; 2 ωM est le champ objet moyen.
- Quand enfin l'angle d'inclinaison objet est égal à ωT, un seul rayon passe par la lucarne de sortie, et entre donc dans l'œil ; 2 ωT est le champ objet total.
Le diamètre d'ouverture de l'oculaire n'intervient pas dans les champs pour deux raisons :
- Il est toujours plus grand que le diamètre de la pupille d'entrée de l'œil, lui même plus grand que que celui du conjugué image de l'objectif à travers l'oculaire ; en conséquence, il ne peut pas être pupille de sortie du système (lunette + œil) ;
- L'oculaire est très proche de la pupille d'entrée de l'œil, et ne peut donc être lucarne de sortie du système (lunette + œil).
Sur l'application Java ci-dessous (Cabri géomètre II et CabriJava) on regardera altenativement le faisceau objet, avec les repères des limites angulaires des champs de pleine lumière, moyen, total et le faisceau image qui rentre tout ou partie dans la pupille d'entrée de l'œil.
Calcul des champs
Les champs images sont calculés à partir de la pupille et de la lucarne de sortie.
Les champs objets sont G fois plus petits.
Notations :
| RPs |
rayon d'ouverture de la pupille de sortie |
| RLs |
rayon d'ouverture de la lucarne de sortie (pupille d'entrée de l'œil) |
| f 'ob |
distance focale image de l'objectif |
| f 'oc |
distance focale image de l'oculaire |
| G |
grossissement de la lunette |
| øob |
diamètre d'ouverture de l'objectif |
| øPeœil |
diamètre de la pupille d'entrée de l'œil |
Un calcul géométrique simple donne les demi-angles de champ images par ordre croissant :
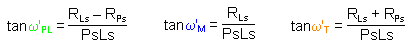
Les champs objets se déduisent des champs images en les divisant par le grossissement G de la lunette.
Les calculs sont développés dans le chapitre suivant (5).
Variation des champs en fonction du diamètre de la pupille d'entrée de l'œil
| Lunette 1 |
Lunette 2 |
| f 'ob = 1,33 m ; Øob = 26 mm ; G = 14 |
f 'ob = 0,98 m ; Øob = 16 mm ; G = 21 |
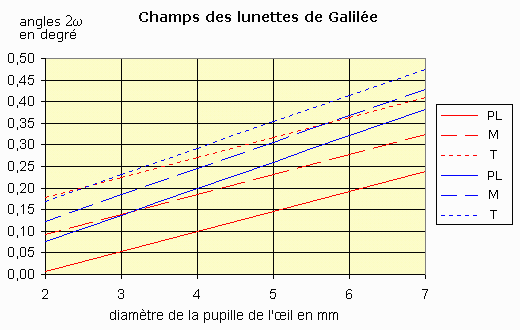
Les courbes ci-dessous représentent les champs objets de pleine lumière, moyen et total pour les deux lunettes de Galilée, en fonction du diamètre de la pupille d'entrée de l'œil.
On fera les remarques suivantes :
- Les champs varient linéairement avec le diamètre de la pupille de l'œil.
- Ils augmentent avec ce diamètre.
- Les champs moyens, les plus significatifs, varient entre 0,1° et 0,43°,
soit entre 6' et 26'.
Jupiter et ses satellites tiennent dans une poignée d'angle de 15 minutes.
De plus l'observation est faite avec une pupille relativement dilatée (5 à 7 mm de diamètre), car le champ est peu éclairé.
On voit donc l'adaptation presque parfaite du champ à ce que Galilée allait découvrir :
il n'a pris que ce qu'il pouvait prendre, mais récoltât quatre diamants !
Variation des champs en fonction du diamètre d'ouverture de l'objectif
Supposons que l'on diaphragme artificiellement l'objectif de la lunette, et que l'on essaye donc de reproduire ce à quoi Galilée fait allusion dans les passages annotés 14 et 15 du Sidereus Nuncius (voir chapitre I).
Les conséquences sont les suivantes :
- La pupille de sortie Ps reste nécessairement pupille de sortie puis qu'elle est encore plus petite que la pupille d'entrée de l'œil, qui reste lucarne de sortie.
- Le champ moyen reste invariant - ce qui ne serait pas le cas si le grossissement était inférieur au grossissement équipupillaire.
- Le champ de pleine lumière diminue, et le champ total augmente symétriquement.
Dans l'application Java qui suit, on observera les variations des trois champs lorsque le bord supérieur de l'objectif est situé au dessus de la limite figurée par le trait marron, et l'invariance du champ moyen, lorsque ce bord est situé en dessous de la limite.
On différenciera de cette façon :
- la lunette hollandaise
(grossissement inférieur au grossissement équipupillaire)
- la lunette de Galilée
(grossissement supérieur au grossissement équipupillaire)
On peut également constater que la luminance apparente du champ de pleine lumière, proportionnelle à l'aire de la pupille d'entrée du système (lunette + œil), reste constante dans le cas de la lunette hollandaise, car c'est le conjugué objet de la pupille de l'œil à travers la lunette qui joue le rôle de pupille d'entrée du système.
champ total (orangé), champ moyen (bleu), champ de pleine lumière (vert)
L'invariance du champ moyen - le champ véritablement pris en compte par l'œil - met en défaut la méthode proposée par Galilée et qui consisterait à diaphragmer l'objectif avec des diaphragmes calibrés pour mesurer les distances angulaires entre les étoiles. Mais il a pourtant bien mesuré ces distances qui séparaient les satellites de Jupiter lors de ses observations. Comment donc a-t-il pu procéder ?
Admettons qu'en bon mathématicien, il avait le compas dans l'œil et, paradoxalement, l'invariance du champ moyen lui était fort utile, car ce champ lui servait de référence. Après avoir reproduit aussi précisément que possible sur le papier les configurations observées, il pouvait ensuite mesurer les diverses proportions et, connaissant la valeur angulaire du champ moyen, en déduire les distances angulaires recherchées.
De façon plus générale, quelqu'un qui a l'habitude de manier la règle et le compas est bien capable de diviser mentalement un champ circulaire en parties égales. Quand bien même Galilée n'aurait pas dessiné les configurations des satellites de Jupiter, il aurait pourtant très certainement mesuré dans sa tête leurs distances respectives, ou en tout cas les proportions de ces distances entre elles !
|