| 9. Logique interne de la lunette |
Pour préciser les conditions de la découverte de la lunette, je vais d'abord développer ce que j'appelle la logique interne de l'instrument, puis je préciserai son histoire pratique, c'est-à-dire les étapes qui, me semble-t-il, ont été successivement franchies au tournant du XVIIe siècle et ont conduit à son invention. Est-il besoin d'un oculaire pour faire une lunette astronomique ? Non, une lentille convergente suffit ! Je vais justifier cette affirmation quelque peu péremptoire puis, dans le paragraphe suivant consacré à l'oculaire, je vais la chiffrer, pour ensuite la modérer. Le schéma ci-dessous illustre le raisonnement. 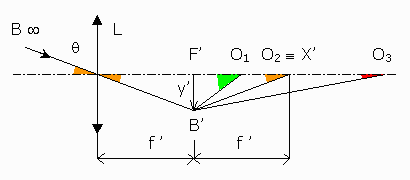
Kepler dans sa Dioptrique décrit parfaitement les conditions d'observation d'une image renversée (Proposition LXXV), résultat repris ensuite dans le célèbre passage sur la lunette avec oculaire convergent - dite aujourd'hui lunette de Kepler - (Problème XXCVI). Quel grossissement espérer avec une seule lentille ? Essayons d'approfondir ce qui vient d'être dit afin de montrer l'intérêt, et le rôle de l'oculaire. Pour observer l'image réelle renversée d'un objet éloigné, donnée par une lentille convergente, il faut que cette image se trouve dans le parcours d'accommodation de l'observateur. Ce parcours est limité du côté de l'œil par le punctum proximum. Appelons p, la distance du proximum à l'œil et bdb, la distance entre la lentille tenue à bout de bras et l'œil. Pour rechercher le grossissement maximum, l'observateur procède le la sorte :
Supposons par ailleurs que l'amplitude d'accommodation suit la courbe de Duane (1922). 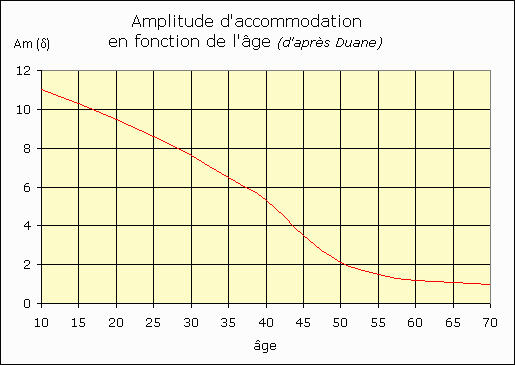 Am = 1/PS, où P est le proximum, et S le sommet de la cornée (PS est exprimé en mètre). Avec le vieillissement, le proximum s'éloigne de l'oeil, et le travail au près devient plus difficile. Il y a presbytie, selon Y. Le Grand, « quand le proximum est plus loin de l'oeil que la distance rapprochée de travail ; celle-ci dépend des occupations du sujet ». Pour quelqu'un qui lit beaucoup, la distance correspond à environ une coudée, c'est-à-dire à la distance qui sépare le coude du poing fermé ; en conséquence la presbytie dépend aussi de la taille du sujet. Dans le cas d'un myope, le proximum étant plus proche de l'oeil, la distance critique est atteinte plus tardivement. Quelques exemples ci-dessous montrent les limites de cette lunette sans oculaire. Les premières courbes traduisent l'équation (3). La variable en abscisse est l'accommodation et le paramètre, la taille (T = 3 bdb). La fonction en ordonnée est le grossissement maximum obtenu avec une seule lentille tenue à bout de bras. 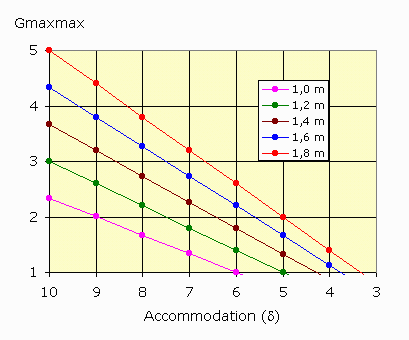 Grossissement optimum en fonction de la taille et de l'accommodation Le grossissement le plus élevé, entre 4 et 5, est obtenu pour de jeunes adultes (accommodation élevée) de grande taille. Les enfants (bras trop courts) et les adultes (vue trop longue) dépasseront difficilement 2,5. - Pour les myopes, les valeurs seront plus élevées. - En ce qui concerne les hypermétropes, deux cas se présentent : pour les faibles et moyens (amétropie inféfieure à 3 dioptries environ), les valeurs du grossissement seront diminuées ; pour les très forts (cas extrêmement rare) le Remotum pourra être utilisé, à la place du Proximum ! Le sujet devra se placer entre le verre et son foyer image ; il bénéficiera d'un grossissement plus élevé. - Enfin, pour les presbytes, aucun grossissement ne sera possible. Sur cette seconde famille de courbes, les tailles sont en abscisse, les accommodations en ordonnée, et le paramètre est la vergence (ou puissance de la lentille tenue à bout de bras pour obtenir le grossissement maximum. La relation se déduit de l'équation (4) : A = 3Dmin/(TDmin - 3) 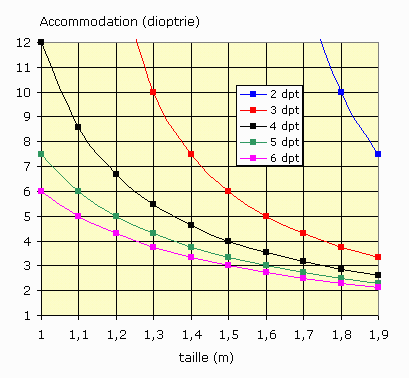 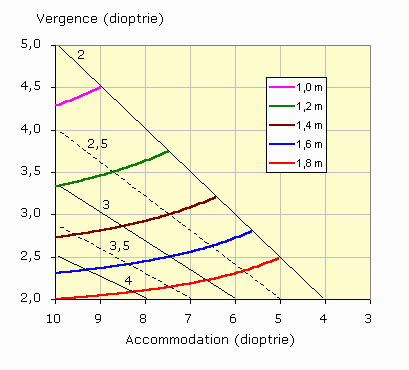 Pourquoi donc un oculaire ? Un problème de bras long et d'accommodation, mais aussi d'alignement. L'oculaire, c'est fait, en quelque sorte, pour se rapprocher de l'image objective sans accommoder. En effet, même dans les meilleures conditions de grossissement (jeune adulte myope de grande taille), l'observation d'une image aérienne avec une forte accommodation ne peut être soutenue longtemps. Une fatigue oculaire apparaît très vite, accompagnée éventuellement de maux de tête. Pour « soulager » l'accommodation, l'image instrumentale doit être rejetée dans le plan rémotal de l'observateur. Dans le cas d'un émmétrope dont le Remotum est à l'infini, l'image objective doit donc se trouver dans le plan focal objet de l'oculaire. Une autre raison de l'oculaire, c'est la nécessité de fixer la position de l'œil de l'observateur. Avec une seule lentille, le placement de l'œil sur l'axe optique n'est pas évident. Le moindre écart place l'objet que l'on veut regarder hors champ. L'oculaire lui est un repère : le petit bout de la lorgnette par lequel il faut regarder. Il matérialise la position de l'œil et facilite ainsi l'observation. 1. Prenons d'abord le cas de l'émmétrope. L'image instrumentale est dans le plan focal objet de l'oculaire.
Il faut tout d'abord préciser que la position de l'œil est indifférente - en ce qui concerne le grossissement -, puisque l'image étant rejetée à l'infini, son diamètre apparent est indépendant de la position de l'observateur. Pour ce qui concerne la focale de l'oculaire, elle est égale à la distance oeil-image objective définie plus haut. Plus cette distance est petite, plus l'effet de rapprochement est important, et plus élevé sera donc le grossissement. Quel oculaire choisir : convergent, ou divergent ? À ce stade du raisonnement, les deux seules différences entre les lunettes de type Galilée (oculaire divergent) et Kepler (oculaire convergent) sont, à grossissement égal, le moindre encombrement de la lunette munie d'un oculaire divergent et l'image droite qu'elle fournit. 2. Dans le cas d'un observateur amétrope sphérique (myope ou hypermétrope, mais pas astigmate), un léger déplacement de l'oculaire, dans le sens positif pour l'hypermétrope, et dans le sens négatif pour le myope, suffit pour amener l'image instrumentale dans le plan remotal de l'observateur. L'oculaire et les champs Comme il a été vu précédemment, les champs de la lunette dépendent des éléments susceptibles de limiter la taille latérale des faisceaux, les diaphragmes. On peut d'abord définir un champ intrinsèque, c'est-à-dire propre à l'instrument. Les deux diaphragmes qui interviennent sont définis par les limites optiques de l'objectif et de l'oculaire - à supposer que ceux-ci soient assimilables à des lentilles minces. La lunette étant supposée afocale, dans l'espace image les deux diaphragmes à prendre en compte sont l'oculaire et le conjugué de l'objectif à travers l'oculaire. Le conjugué image de l'objectif à travers l'oculaire est construit à partir d'un rayon intermédiaire passant par le foyer objet de l'oculaire et réfracté parallèlement à l'axe optique, et un rayon passant par le centre optique de l'oculaire et réfracté sans déviation. Si l'on considère une lunette de Kepler (K) et une lunette de Galilée (G) de mêmes caractéristiques axiales et transversales - au signe près de la focale de l'oculaire - les pupilles de sortie ont même diamètre et sont placées à la même distance algébrique du foyer image de l'oculaire. (La démonstration se fait à partir des formules de Newton.) On obtient : ØPs = ØOb/G et F'ocPs = f 'ob/G. 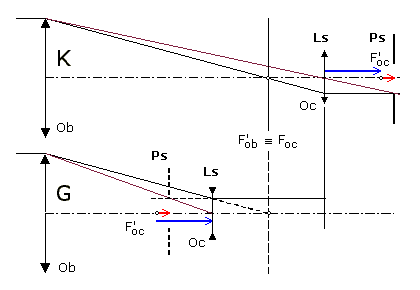 Comme les lunettes sont afocales et les objets à l'infini, les faisceaux images sont parallèles et les trois demi-champs angulaires (champs apparents) sont obtenus en joignant les bords et le centre de la pupille de sortie au bord de la lucarne de sortie. Sur les schémas ci-dessus on a supposé que l'objectif était diaphragme d'ouverture, ce qui est généralement le cas pour une lunette de Kepler, ainsi que pour une lunette de Galilée au sens défini plus haut (fort grossissement). Il apparaît clairement que pupille et lucarne de sortie sont plus proches pour la lunette de Galilée (distance |f 'oc| - |f 'oc|/G, flèche bleue moins flèche rouge) que pour la lunette de Kepler (distance f 'oc + f 'oc/G, flèche bleue plus flèche rouge). Il s'en suit que les champs intrinsèques de la lunette de Galilée sont plus grands que ceux de la lunette de Kepler. Toutefois, lorsque le grossissement est élevé, la différence de distance, égale à deux fois la distance focale de l'oculaire divisée par le grossissement de la lunette, peut être négligée par rapport à la focale de l'oculaire, et les champs intrinsèques des deux lunettes sont approximativement égaux. La lunette de Galilée semblerait donc l'emporter haut la main sur la lunette de Kepler par :
En effet, les champs d'une lunette n'ont de sens, que si l'on prend en compte l'observateur, sa position par rapport à l'oculaire, et le diamètre de la pupille d'entrée de son œil. Et là, la situation s'inverse pour les champs : c'est la lunette de Kepler qui prend l'avantage sur la lunette de Galilée, comme nous le montrent les exemples ci-dessous.
Les champs objets de pleine lumière, moyen et total sont en degré. Les deux lunettes ont les caractéristiques définies au chapitre 4. La pupille de l'œil a un diamètre de 5,5 mm. Le nombre entre parenthèses dans les colonnes K et G représente la distance entre l'oculaire et la pupille d'entrée de l'œil de l'observateur. Pour les lunettes de Kepler elle est égale à la distance Oc-Ob', et pour les lunettes de Galilée, elle est choisie nulle (celle qui donne champs les plus grands), ou égale à 10 mm, ce qui est plus réaliste, car il faut tenir compte des cils qui maintiennent l'œil à une certaine distance de l'oculaire. Le gain de champ moyen pour la lunette de Kepler, en comparaison avec celle de Galilée, est d'environ 75% pour le première lunette et de 100% pour la seconde. |
|||||||||||||||||||||||||||||||||||