Polycycles

Ce sont les problèmes de formes de calibres de verres de lunettes – déjà abordés plus haut – qui m'ont orienté vers l'article de François Rideau sur les polycycles (12 avril 2005). Il fait dans cet article référence à ce que Bernard Koch appelle des (anses de panier), propose ce nom de polycycle, et donne de ces courbes particulières une théorie mathématique générale.

A. Définition, propriétés et construction des polycycles

Un polycycle est une courbe fermée composée d'arcs de cercles raccordés tangentiellement.

Deux cas de figure se présentent selon que le nombre de points n délimitant les arcs de cercles est pair ou impair.

n impair : il n'existe qu'un seul polycycle passant par les points donnés.
n pair : il existe une infinité de polycycles passant par les points donnés, ou aucun.

Avant d'étudier ces deux cas de figure, voyons comment se construit le premier arc de polycycle.

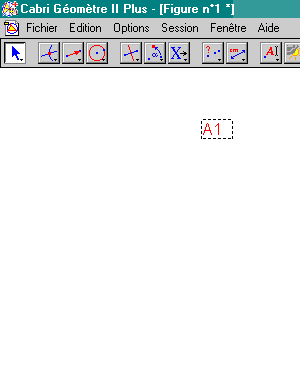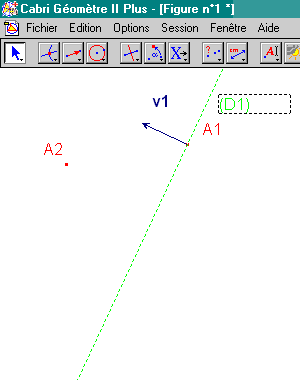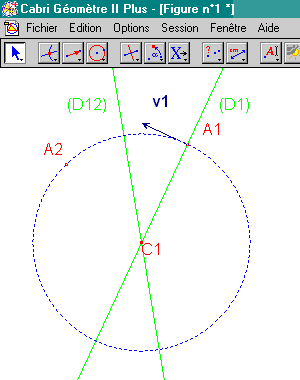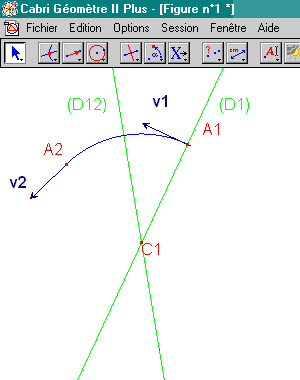
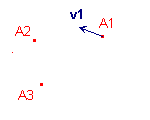
On associe au premier point A₁ un vecteur v₁ d'origine A₁, de module arbitraire et dont la direction caractérise la tangente à l'arc de polycycle en A₁.
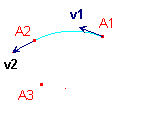
On recherche ensuite la rotation qui transforme v₁ en un vecteur v₂, tangent à l'arc en A₂. Le sens de la rotation est fixé par la direction du vecteur v₁.

Les constructions successives apparais- sent sur cette image gif animée.

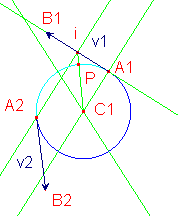
1. Point A₁.
2. Point A₂.
3. Vecteur v₁ d'origine A₁.
4. (D₁) = Perpendiculaire à v₁ en A₁.
5. (D12) = Médiatrice de A₁A₂.
6. C₁ = intersection de (D₁) et (D₁₂).
7. Cercle de centre C₁ et de rayon C₁A₁.
8. Vecteur v₂ obtenu par rotation de v₁, dans la rotation de centre C₁ et d'angle (A₁C₁A₂).
9. Sélection du petit arc (car l'angle de rotation est inférieur à 180°).

3 exemples de macro-commandes dessinant l'arc de cercle (on se donne A₁, A₂ et v₁).

Première mouture J.H. (macro PolycycleJH0)	Figures 1 & 2
Macro Cabri II Plus vers. MS-Windows 1.2.5 PolycycleJH1, no name Help: " vecteur vk, point Ak+1 " Mth: 0 CN:2, ON:19, FN:6, PO:11 CT: vector, CS 2, default settings, point, CS 0, default settings, Const: Perp, Mth:0, 0, CN:2, VN:4, Const: 1 3 Perpendiculaire (5) à v₁ en A₁ PBiss, Mth:0, 0, CN:2, VN:4, Const: 1 4 Médiatrice (6) de A₁A₂ Int, Mth:0, 0, CN:2, VN:1, int ind:0, Const: 5 6 Intersection C₁ (7) de 5 et 6 Cir, Mth:1, 0, CN:2, VN:2, Const: 7 1 Cercle (8) de centre C₁ passant par A₁ (1) Ray, Mth:1, 0, CN:2, VN:3, Const: 1 2 Demi-droite (9) d'origine A₁ (1) et passant par l'extrémité B₁ (2) de v₁ Sym, Mth:0, 0, CN:2, VN:1, Const: 2 1 Symétrique B'₁ (10) de B₁ (2) par rapport à A₁ (1) Ray, Mth:1, 0, CN:2, VN:3, Const: 1 10 Demi-droite (11) A₁B'₁ Perp, Mth:0, 0, CN:2, VN:4, Const: 4 9 Perpendiculaire (12) menée de A₂, à la demi-droite (9) Int, Mth:0, 0, CN:2, VN:1, int ind:0, Const: 12 9 Intersection i de 12 et de 9 Seg, Mth:0, 0, CN:2, VN:2, Const: 13 7 Segment (14) iC₁ Int, Mth:0, 1, CN:2, VN:1, int ind:0x10000, Const: 14 8, invisible, Intersection P (15) du segment (14) avec le cercle (8) Arc, Mth:0, 1, CN:3, VN:5, Const: 1 15 4, default settings, Arc (1^er cas) A₁PA₂ 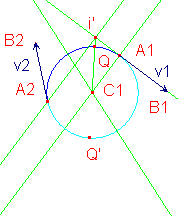Int, Mth:0, 0, CN:2, VN:1, int ind:0, Const: 12 11 Intersection i' de la perpendiculaire (12) avec la deuxième demi-droite (11) Seg, Mth:0, 0, CN:2, VN:2, Const: 17 7 Segment (18) i'C₁ Int, Mth:0, 0, CN:2, VN:1, int ind:0x10000, Const: 18 8 Intersection Q (19) du segment (18) avec le cercle (8) Sym, Mth:0, 1, CN:2, VN:1, Const: 19 7, invisible, Symétrique Q' (20) de Q (18) par rapport à C₁ Arc, Mth:0, 1, CN:3, VN:4, Const: 1 20 4, default settings, Arc (2^ème cas) A₁Q'A₂ Rot, Mth:1, 1, CN:5, VN:1, Const: 2 7 1 7 4, invisible, B₂ (22), résultat de la rotation de B₁ (2) par rapport à C₁ (7) dans une rotation d'angle A₁C₁A₂ (174) Vec, Mth:0, 1, CN:2, VN:2, Const: 4 22, default settings, Vecteur A₂B₂ Remarque : Il est nécessaire de traiter les deux cas de figure (arc inférieur à un demi-cercle, arc supérieur à un demi-cercle). D'où le rôle du symétrique de la demi-droite d. Cela nécessite de modifier la direction du vecteur V(A) – le plus commode est de prendre un vecteur de sens opposé – et d'appliquer la suite de la procédure. La construction est alourdie. La macro comporte 19 lignes d'instructions (décomptées après le Const:) !
Version F.Rideau légèrement modifiée (macro PolycycleFR)	Figure 3
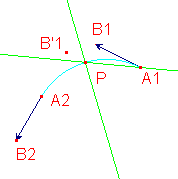
PolycycleFR, no name Help: "Vecteur et point" Mth: 0 CN:2, ON:7, FN:4, PO:5 CT: vector, CS 2, default settings, point, CS 0, default settings, Const: Biss, Mth:0, 0, CN:3, VN:4, Const: 4 1 2 Bissectrice de l'angle A₂A₁B₁ PBiss, Mth:0, 0, CN:2, VN:4, Const: 1 4 Médiatrice de A₁A₂ Int, Mth:0, 1, CN:2, VN:1, int ind:0, Const: 5 6, invisible, L'intersection des deux donne le point médian de l'arc (deux angles inscrits égaux interceptant des arcs égaux !) Refl, Mth:0, 0, CN:2, VN:1, Const: 2 6 B'₁ est le symétrique de B₁ par rapport à la médiatrice Sym, Mth:0, 1, CN:2, VN:1, Const: 8 4, invisible, Et B₂, le symétrique de B'₁ par rapport à A₂ !! Vec, Mth:0, 1, CN:2, VN:2, Const: 4 9, default settings, Arc, Mth:0, 1, CN:3, VN:4, Const: 1 7 4, default settings, Remarque : On passe de 19 lignes d'instruction à 7 : soit environ trois fois moins !! La construction du cercle est ici inutile.
Deuxième mouture J.H. (macro PolycycleJH1)	Figure 4
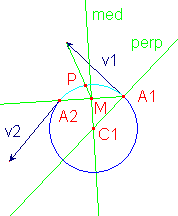
Macro Cabri II Plus vers. MS-Windows 1.2.5 PolycycleJH2, no name Help: " vecteur vk d'origine Ak, point Ak+1 " Mth: 0 CN:2, ON:12, FN:5, PO:7 CT: vector, CS 2, default settings, v₁ est associé aux trois nombres : 1 (origine), 2(extrémité), 3(le vecteur lui-même) point, CS 0, default settings, Il est associé au nombre 4 Const: Perp, Mth:0, 0, CN:2, VN:4, Const: 1 3 Comme précédemment, perpendiculaire au vecteur (3) en son origine (1) PBiss, Mth:0, 0, CN:2, VN:4, Const: 4 1 Puis médiatrice de A₂A₁ (associée à 6) Int, Mth:0, 0, CN:2, VN:1, int ind:0, Const: 5 6 Recherche du centre du cercle, intersection de la perpendiculaire et de la médiatrice Cir, Mth:1, 0, CN:2, VN:2, Const: 7 4 Et tracé du cercle Ray, Mth:1, 0, CN:2, VN:3, Const: 1 4 Demi-droite A₁A₂ ; elle est associée au nombre 9 Int, Mth:0, 0, CN:2, VN:1, int ind:0, Const: 6 9 Intersection M ((10) de la médiatrice (6) et de la demi-droite (9) Seg, Mth:0, 0, CN:2, VN:2, Const: 2 10 Segment (11) reliant l'extrémité B1 (2) de v₁ et le point M (10) Int, Mth:0, 1, CN:2, VN:1, int ind:0x10000, Const: 11 8, invisible, Intersection P (12) du segment (11) avec le cercle (8) Rot, Mth:1, 1, CN:5, VN:1, Const: 2 7 1 7 4, default settings, B₂ (13), obtenu par rotation du point B₁ autour de C₁ de l'angle A₁C₁A₂ Vec, Mth:0, 1, CN:2, VN:2, Const: 4 13, default settings, Tracé du vecteur v₂ Arc, Mth:0, 1, CN:3, VN:4, Const: 1 12 4, default settings, Tracé de l'arc recherché A₁PA₂ Remarque : 11 lignes d'instructions : c'est un peu mieux que ma première tentative !!! Les deux cas de figure sont traités en une seule fois.

On dispose d'une première macro-commande, avec trois variantes (parmi d'autres), qui nous permet, de proche en proche, de construire des arcs de polycycles. Mais pour former un polycycle selon la définition (courbe fermée), il va falloir les boucler.
Le dernier point A_n atteint, il doit être relié au premier A₁ par un arc de cercle. Or on dispose alors de deux points et de leurs vecteurs associés v_n et v₁. Pour que le dernier arc fasse raccord tangentiel, il faut que les deux perpendiculaires aux vecteurs en A_n et A₁ et la médiatrice de A_nA₁ soient concourantes : ce qui est loin d'aller de soi.

La recette est la suivante pour boucler le polycycle (d'ordre pair ou impair) :

On se fixe les n - 1 premiers points,
Ainsi que le premier vecteur v₁.
On construit les n - 2 vecteurs v₂, v₃, … v_{n - 1} et les arcs de cercles correspondants.
On trace le cercle passant par A₁, dont le centre est le point d'intersection des médiatrices de
A_{n - 1}A₁ et de B_{n - 1}B₁. (Ce cercle est associé à la rotation qui transforme v_{n - 1} en v₁.)
On choisit un point quelconque A_n sur ce cercle.
On construit le vecteur v_n et l'arc de cercle correspondant.
On termine la boucle ; le vecteur v_{n + 1} se superpose au vecteur v₁.

La macro complémentaire ci-après permet de créer le dernier point du polycycle.

Macro Cabri II Plus vers. MS-Windows 1.2.5

PolycycleJH2, no name

Help:
"extrémités des vecteurs n - 2 et 1 (4 points : dans l'ordre An-2, Bn-2, A1, B1)"
Mth: 0
CN:4, ON:5, FN:3, PO:4
CT:
point, CS 0, default settings,
An - 1
point, CS 0, default settings,
Bn - 1
point, CS 0, default settings,
A1
point, CS 0, default settings,
B1
Const:
PBiss, Mth:0, 0, CN:2, VN:4, Const: 1 3
médiatrice de An - 1A1
PBiss, Mth:0, 0, CN:2, VN:4, Const: 4 2
médiatrice de Bn - 1B1
Int, Mth:0, 1, CN:2, VN:1, int ind:0, Const: 5 6, default settings,
Intersection des deux médiatrices (centre du cercle recherché)
Cir, Mth:1, 1, CN:2, VN:2, Const: 7 3, default settings,
Tracé du cercle
Pt/, Mth:3, 1, CN:1, VN:2, Const: 8, color:Bl,
Point courant sur ce cercle

B. Exemples

1. Construction d'un polycycle d'ordre 4


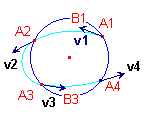
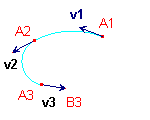
Données	PolycycleJH1.mac (v1, A2)	PolycycleJH1.mac (v2, A3)

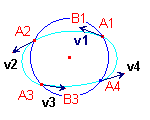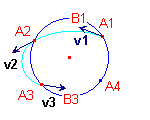
PolycycleJH2.mac (A3A1, B3B1)	PolycycleJH1.mac (v3, A4)	PolycycleJH1.mac (v4, A1)

2. Polycycle d'ordre pair

La méthode explicitée au dessus peut être généralisée. Le dodécacycle ci-dessous a été généré à partir de 11 points, le 12ème (obtenu avec la macro PolycycleJH2.mac) étant contraint à rester solidaire du cercle bleu.

En faisant tourner B1 autour de A1, on génère une infinité de polycycles passant par les 12 points (A1, … A12).

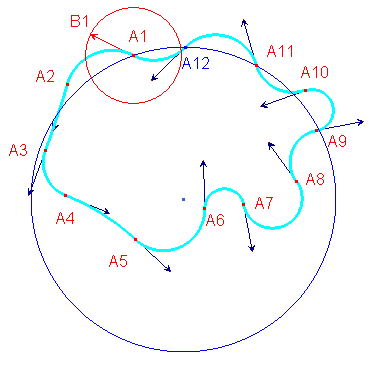
Remarque :

Si l'on essaie de tracer un polycycle d'ordre n pair à partir de la totalité de ses points, on n'y arrive pas (sauf déjà précisé plus haut hasard plus qu'heureux). Le vecteur v_n+1 forme avec le vecteur v₁ un angle a invariant. Il suffit en effet de modifier l'orientation de v₁ pour constater que l'orientation de v_n+1 change avec conservation de l'angle des deux vecteurs.

3. Construction d'un polycycle d'ordre impair

Il y a dans ce cas deux possibilités.

Les n points sont imposés.
On fait une première tournée de la macro PolycycleJH1.mac et l'on constate – sauf hasard plus qu'heureux – que le vecteur v_{n + 1} ne se superpose pas avec v₁.
Il faut alors remplacer v₁ par le vecteur w₁ = v₁ + v_{n + 1}, et relancer la tournée.
À l'arrivée on constate – là le hasard n'entre plus en ligne de compte – que w_{n + 1} est superposé avec w₁. La boucle est bien bouclée et le seul et unique polycycle obtenu.
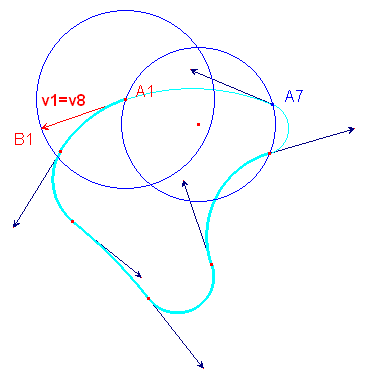
Sur la figure ci-après, le premier tour donne la courbe bleue, et le second, et dernier, la courbe verte, c'est-à-dire le polycycle recherché.
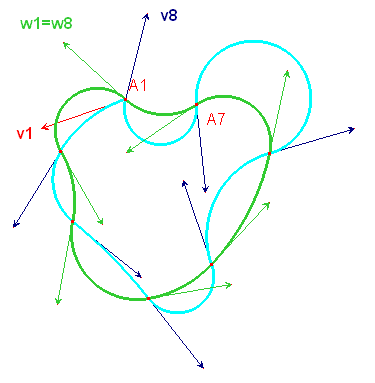
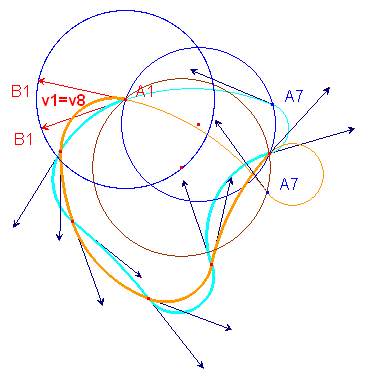
Le nième point n'est pas imposé.
On procède alors avec la macro PolycycleJH2.mac pour construire le nième point.
Quand on fait tourner B₁ autour de A₁, le point créé A_n se déplace avec le cercle auquel il est lié. Le polycycle est évidemment modifié (c'est ce que l'on voit sur la deuxième figure ou deux positions de B1 ont été représentées avec les polycycles bleu et orange correpondants.

C. Application à l'approximation d'une ellipse

Revenons aux anses de panier et essayons d'approximer une ellipse par un polycycle d'ordre 8. Pourquoi d'ordre 8, parce que du fait des deux symétries axiales d'une ellipse par rapport à ses axes rectangulaires, l'approximation la plus simple va utiliser deux arcs de cercles par quart d'ellipse, soit 8 au total.

Les résultats ci-après recoupent le travail de François Rideau dans son article :
"Anses de panier" du 2 février 2005.

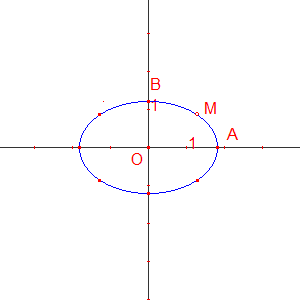	Un point M est choisi arbitrairement sur le premier quart d'ellipse. Les 8 points du polycycle sont : - les extrémités des axes ; - le point M et ses symétriques successifs par rapport aux axes de l'ellipse.
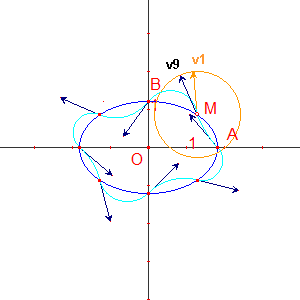	Le point M est le premier point du polycycle. On lui associe un vecteur (orange sur la figure) de module et de direction arbitraire. Et l'on applique 8 fois la macro-commande PolycycleJH1. Bien évidemment le vecteur v₉ ne coïncide pas avec v₁.
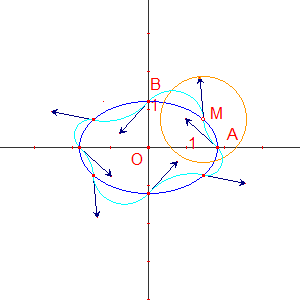	En déplaçant M sur le quart d'ellipse, on trouve une seule position pour laquelle les deux vecteurs v₁ et v₉ sont confondus. Le polycycle réalisé ne correspond pas à l'ajustement souhaité, car il ne possède pas les symétries de l'ellipse.
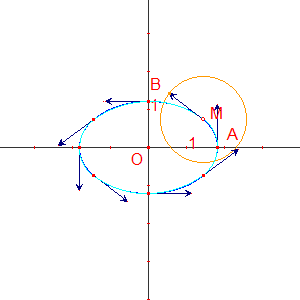	En modifiant l'orientation de v1, on arrive à un polycycle de mêmes axes de symétrie que l'ellipse. Les vecteurs v aux extrémités des axes de l'ellipse sont alors perpendiculaires à ceux-ci. L'ajustement est de bonne qualité, à condition que le rapport des axes (grand/petit) ne s'écarte pas trop de l'unité.
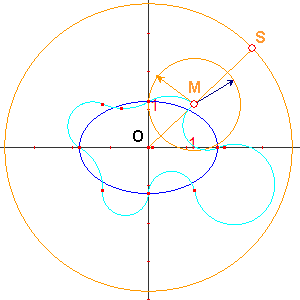	Pour trouver la position exacte du point sur le quart d'ellipse on procède à une généralisation. On suppose le point M quelconque et l'on recherche le lieu des points M tels que les 8 points (les 4 extrémités des diamètres de l'ellipse, M et ses 3 symétriques par rapport aux axes) correspondent à un polycycle (et donc à une infinité puis le nombre de points est pair). Le paramétrage de la position de M se fait par un point mobile sur un segment OS, lui même tournant autour du point O. On crée ensuite un point conditionnel en M : m, tel que m n'existe que si la distance entre les extrémités de v₁ et v₉ est inférieure à une certaine valeur.
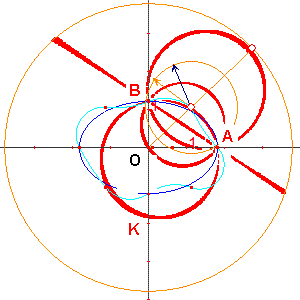	On a choisi pour distance maximale entre les extrémités de v₁ et v₉ : 0,1 cm. Le lieu de m par rapport à M est mis en mode trace (il clignote alors) et l'on lance par la fonction animation. Cela permet de faire apparaître le lieu de M. Ce lieu est constitué d'une droite AB et de trois cercles : - le premier a pour diamètre AB ; - le deuxième passe par A, B et le point K, tel que : OK = OA ; - le troisième est symétrique du deuxième par rapport à AB.
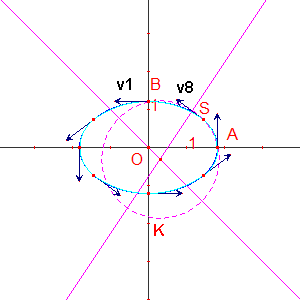	Pour construire le polycycle recherché, il faut tracer le deuxième cercle et chercher son intersection S avec le premier quart d'ellipse. Il est ensuite plus commode, pour générer ce polycycle, de partir du point B, où le vecteur v est perpendiculaire à l'axe des y. L'application de la macro-commande PolycycleJH1 donne, appliquée 8 fois, le polycycle.
	Dans le cas présent, un zoom sur la zone au voisinage de S montre les positions respectives de l'ellipse et des arcs de polycycle. L'arc à gauche de S est à l'intérieur de l'ellipse et l'arc à droite, à l'extérieur.