Macro-commandes Bézier 1 2 & 3

Ces trois macros permettent de boucler des courbes de Bézier (3 au moins). A. Principe de la construction Les deux premières macro-commandes sont commentées (en rouge) à partir des fichiers texte. La troisième pourra facilement être commentée, à titre d'exercice. Il est recommandé de se munir d'un crayon et d'une feuille de papier, ou alors, de travailler directement sur CABRI. On rappelle que chaque élément géométrique est numéroté, dans l'ordre de son apparition. Dans ce qui suit, les lignes des fichiers texte consacrées aux icônes, et qui ne présentaient pas d'intérêt pour l'analyse de la construction, ont été supprimées. Bézier1, no name Help: ''Pointer 3 points'' Mth: 0 CN:3, ON:8, FN:1, PO:7 CT: point, CS 0, color:B, thicker, point 1 point, CS 0, color:B, thicker, point 2 point, CS 0, color:B, thicker, point 3 Const: Seg, Mth:0, 0, CN:2, VN:2, Const: 1 2 segment 4 joignant les points 1 et 2 Pt/, Mth:1, 0, CN:1, VN:2, Const: 4 point courant 5 sur segment 4 Lgth, Mth:1, 0, CN:2, VN:1, Const: 1 5 mesure de la distance 6 entre les points 1 et 5 Lgth, Mth:1, 0, CN:2, VN:1, Const: 1 2 mesure de la distance 7 entre les points 1 et 2 Formula, Mth:0, 0, CN:2, VN:1, Const: 6 7, formula: a/b calcul du rapport 8 = (distance 6/distance 7) Dil, Mth:0, 0, CN:3, VN:1, Const: 3 2 8 homothétique 9 du point 3, dans une homothétie de sommet le point 2 et de rapport 8 Dil, Mth:0, 0, CN:3, VN:1, Const: 9 5 8 homothétique 10 du point 9, dans une homothétie de sommet le point 5 et de rapport 8 Locus, Mth:0, 1, CN:2, VN:12, lk pts, locus, nb pts: 12, Const: 5 10, thicker, lieu du point 10 par rapport au point courant 5 (12 points reliés) Bézier2, no name Help: ''trois points précédents + 4ème point'' Mth: 0 CN:4, ON:14, FN:2, PO:13 CT: point, CS 0, color:B, thicker, point 1 point, CS 0, color:B, thicker, point 2 point, CS 0, color:B, thicker, point 3 point, CS 0, color:B, thicker, point 4 Const: Line, Mth:1, 0, CN:2, VN:4, Const: 2 3 droite 5 passant par les points 2 et 3 Line, Mth:1, 0, CN:2, VN:4, Const: 1 3 droite 6 passant par les points 1 et 3 Par, Mth:0, 0, CN:2, VN:4, Const: 4 6 parallèle 7 à droite 6, passant par le point 4 Int, Mth:0, 0, CN:2, VN:1, int ind:0, Const: 5 7 intersection 8 des droites 5 et 7 Seg, Mth:0, 0, CN:2, VN:2, Const: 3 8 segment 9 joignant les points 3 et 8 Pt/, Mth:1, 1, CN:1, VN:2, Const: 9, color:B, thicker, point courant 10 sur segment 9 Le déplacement de ce point est choisi de façon quelque peu arbitraire sur le segment 9. On aurait pu choisir un autre segment porté par la même droite. Seg, Mth:0, 0, CN:2, VN:2, Const: 3 10 segment 11 joignant les points 3 et 10 Pt/, Mth:1, 0, CN:1, VN:2, Const: 11 point courant 12 sur segment 11 Lgth, Mth:1, 0, CN:2, VN:1, Const: 3 12 mesure de la distance 13 entre les points 3 et 12 Lgth, Mth:1, 0, CN:2, VN:1, Const: 3 10 mesure de la distance 14 entre les points 3 et 10 Formula, Mth:0, 0, CN:2, VN:1, Const: 13 14, formula: a/b calcul du rapport 15 = (distance 13/distance 14) Dil, Mth:0, 0, CN:3, VN:1, Const: 4 10 15 homothétique 16 du point 4, dans une homothétie de sommet le point 10 et de rapport 15 Dil, Mth:0, 0, CN:3, VN:1, Const: 16 12 15 homothétique 17 du point 16, dans une homothétie de sommet le point 12 et de rapport 15 Locus, Mth:0, 1, CN:2, VN:12, lk pts, locus, nb pts: 12, Const: 12 17, thicker, lieu du point 17 par rapport au point courant 12 (12 points reliés) Bézier3, no name Help: ''Deux derniers points + deux premiers points'' Mth: 0 CN:4, ON:11, FN:2, PO:2 CT: point, CS 0, color:B, thicker, point, CS 0, color:B, thicker, point, CS 0, color:B, thicker, point, CS 0, color:B, thicker, Const: Line, Mth:1, 0, CN:2, VN:4, Const: 4 3 Line, Mth:1, 0, CN:2, VN:4, Const: 1 2 Int, Mth:0, 1, CN:2, VN:1, int ind:0, Const: 5 6, color:B, thicker, Seg, Mth:0, 0, CN:2, VN:2, Const: 2 7 Pt/, Mth:1, 0, CN:1, VN:2, Const: 8 Lgth, Mth:1, 0, CN:2, VN:1, Const: 2 9 Lgth, Mth:1, 0, CN:2, VN:1, Const: 2 7 Formula, Mth:0, 0, CN:2, VN:1, Const: 10 11, formula: a/b Dil, Mth:0, 0, CN:3, VN:1, Const: 3 7 12 Dil, Mth:0, 0, CN:3, VN:1, Const: 13 9 12 Locus, Mth:0, 1, CN:2, VN:12, lk pts, locus, nb pts: 12, Const: 9 14, thicker, B. Mode d'emploi Il est nécessaire de travailler avec k courbes : k ³ 3. On applique la première macro-commande (Bézier 1) en sélectionnant 3 points (appelons-les 1, 2 et 3). La deuxième macro-commande (Bézier 2) est ensuite appliquée aux quatre points 1, 2, 3 et le suivant (5, car cette macro crée le point 4). On réitère cette opération (k - 2) fois. Enfin, pour boucler le tout, on applique la troisième macro-commande (Bézier 3) qui nécessite la sélection des deux derniers points et des deux premiers. C. Exemple Quatre courbes de Bézier sont bouclées (voir fichier joint). 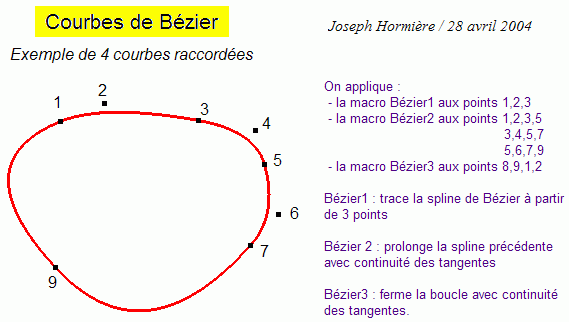Un petit jeu du type casse-tête consiste à faire entrer la boucle dans un anneau (voir ci-dessous), en agissant sur tous les points, à l'exception du dernier. 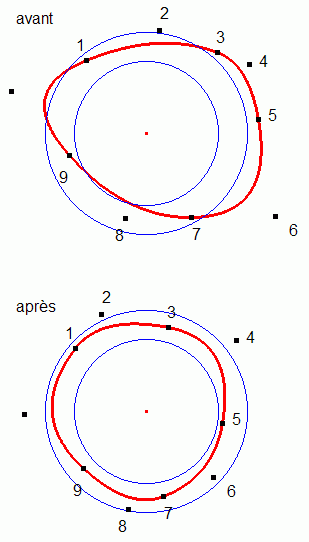Les matheux pourront rechercher l'anneau d'épaisseur minimum, quand le grand cercle est fixé. Si les rayons des deux cercles concentriques sont r et R, la solution (R - r)/R minimum doit dépendre du nombre de courbes raccordées : cf. polygones et flèche des courbes de Bézier à Macro-commande Bézier 4 (la flèche est égale à la demi-hauteur du triangle formé par les trois points définissant la courbe, hauteur associée au point A ; voir ci-dessous).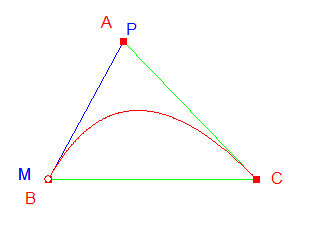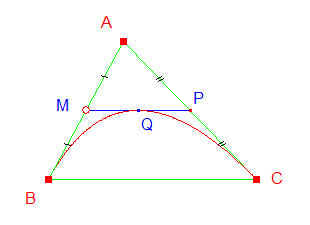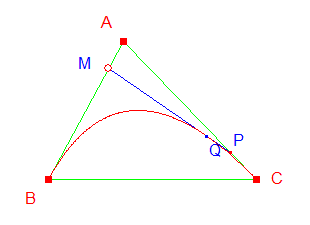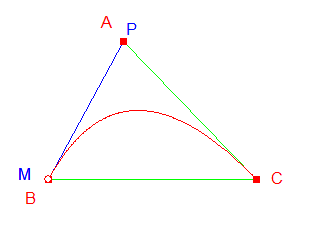